NZC - Mathematics and statistics (Phase 2)

Progress outcome and teaching sequence for Phase 2 (year 4-6) of the Mathematics and statistics Learning Area. From 1 January 2025 this content is part of the statement of official policy relating to teaching, learning, and assessment of Mathematics and statistics in all English medium state and state-integrated schools in New Zealand.

NZC – Mathematics and statistics

Years 0‑8

NZC – Mathematics and statistics

Phase 1 – Years 0‑3

NZC – Mathematics and statistics

Phase 2 – Years 4‑6

NZC – Mathematics and statistics

Phase 3 – Years 7‑8

Page quick links

Mathematics and statistics: Phase 2 (Years 4-6)

Progress outcome by the end of year 6

Teaching sequence – Phase 2 (Years 4-6)

About this resource

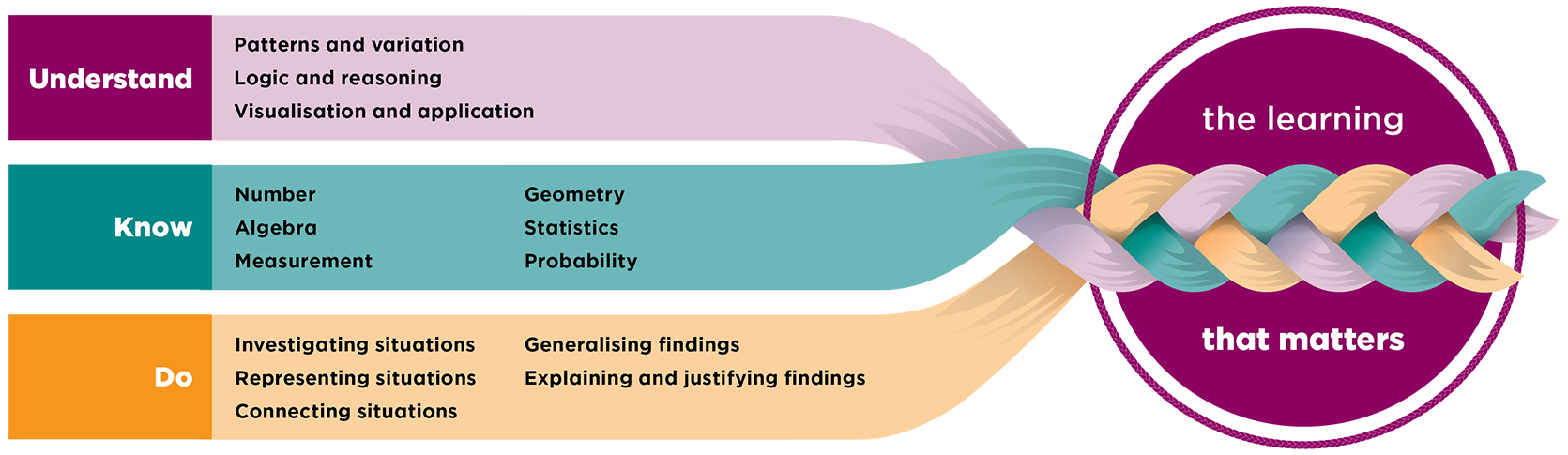
This page provides the progress outcome and teaching sequence for Phase 2 (Year 4-6) of the Mathematics and statistics learning area of the New Zealand Curriculum, the official document that sets the direction for teaching, learning, and assessment in all English medium state and state-integrated schools in New Zealand. In mathematics and statistics, students explore relationships in quantities, space, and data and learn to express these relationships in ways that help them to make sense of the world around them. Other parts of the learning area are provided on companion pages.

We have also provided the Maths Years 0-8 curriculum in PDF format. There are different versions available for printing (spreads), viewing online (single page), and to view by phase. You can access these using the icons below. Use your mouse and hover over each icon to see the document description.

Reviews

Te Mātaiaho | The New Zealand Curriculum

Mathematics and statistics: Phase 2 – Years 4‑6

Expanding horizons of knowledge, and collaborating
Te whakawhānui i ngā pae o te mātauranga, me te mahi tahi

Progress outcome by the end of year 6

The critical focus of phase 2 is for all students to expand their horizons of knowledge and their collaboration with others. Students use a variety of representations to model number operations and to solve word problems. They connect and extend their reasoning about whole numbers to fractions and decimals, and they visualise and classify angles, using benchmarks to justify their classifications. Students also apply their understanding of number operations to reasoning about perimeter and area and to investigating variations in patterns, shapes, and data.

The phase 2 progress outcome describes the understanding, knowledge, and processes that students have multiple opportunities to develop over the phase.

The phase 2 progress outcome is found in the table below.

Understand

As students build knowledge through their use of the mathematical and statistical processes, they develop their understanding of the following.

Patterns and variation | Ngā ia auau me ngā rerekētanga

The world is full of patterns and is defined by a multitude of relationships in which change and variation occur. Mathematics and statistics provide structures that are useful for noticing, exploring, and describing different types of patterns and relationships, enabling us to generate insights or make conjectures.

Logic and reasoning | Te whakaaro arorau me te whakaaroaro

By engaging with mathematical concepts, we develop logical reasoning and critical-thinking skills that enable us to evaluate information, question assumptions, and present arguments with clarity. Statistical reasoning from observation and theory allows us to differentiate what is probable from what is possible and to draw reliable conclusions about what is reasonable.

Visualisation and application | Te whakakite me te whakatinana

The visualisation of mathematical and statistical ideas profoundly influences how we perceive, understand, and interact with abstract concepts. Application in mathematics and statistics involves creating structures and processes that help us understand complex situations, enabling better decision making and communication of ideas.

Know

Number | Mātauranga tau

By the end of this phase, students know that in our number system each place value is a power of 10, and this continues infinitely. To the right, the system continues past the ones column to create decimals (tenths, hundredths, thousandths); the decimal point marks the column immediately to the right as the tenths column. Estimation and rounding support checking the reasonableness of solutions of operations involving whole numbers, fractions, and decimals. Students know that to evaluate expressions that have more than one operation, operations inside brackets (i.e., grouped together) are done first. If there are multiplication and division, these are then done in left-to-right order; finally, addition and subtraction are also done in left-to-right order. Division can be partitive (the number of shares is known) or quotitive (the size of the shares is known).

Students come to recognise the properties of number operations. The additive identity is 0 (e.g., 3 + 0 = 3) and the multiplicative identity is 1 (e.g., 5 × 1 = 5). The commutative property (e.g., 3 × 5 = 5 × 3) and associative property (e.g., 3 × (4 × 6) = (3 × 4) × 6) apply to addition and multiplication but not to subtraction and division. The distributive property (e.g., 2 × (6 – 4) = 2 × 6 – 2 × 4) applies to multiplication over addition and subtraction.

Students also come to know that fractions can result from one number divided by another (the quotient), operate on quantities, and be larger than 1. Improper fractions can also be written as a mixed number, represented as a whole number and a fraction, combined with a hidden addition. In simplified fractions, the numerator and denominator have no common factors; if the denominator of a simplified fraction is 1, then it can be written as a whole number. Decimals are fractions that have powers of 10 as their denominators, and they can be written as numbers using a decimal point. A percentage is a fraction with a denominator of 100.

Algebra | Taurangi

By the end of this phase, students know that the equal (=) and inequality (<, >) signs show relationships, and that applying the same operation to both sides of an equation preserves the balance of the equation. Students know that in a pattern, the relationship between the ordinal position and its corresponding element can be used for finding the pattern rule. Any element can be found by knowing its position, and any position can be found from its corresponding element. Tables and XY graphs provide a way of organising the positions and elements of a pattern to reveal relationships or rules. An algorithm is an ordered list of instructions for solving a problem.

Measurement | Ine

By the end of this phase, students know that, like our place-value number system, the metric measurement system is based on powers of 10 and that appropriate metric units are used to quantify length, area, volume, capacity, mass (weight), and temperature. Measurements can include whole units and parts of units. Different measurement tools and scales use different-sized units, and the unit must be recorded with the amount. Duration is the amount of time it takes for an event to occur. Angles are a measure of turn and can use the unit of degrees.

Geometry | Āhuahanga

By the end of this phase, students know that two- and three-dimensional shapes have consistent properties that can be used to define, compare, classify, predict, and identify relationships between shapes. Shapes can be transformed by rotation, reflection, translation, and resizing (when they are enlarged or reduced). Lines of symmetry can be horizontal, vertical, and diagonal. Three-dimensional shapes can be composed of connected two- or three-dimensional shapes. Students also know that position can be described using known environmental features and elements from the natural world. Maps can use grid references to specify the position of locations, scales to show distances, and connections to show pathways.

Statistics | Tauanga

By the end of this phase, students know that data about people and the natural world must be collected, used, and stored carefully. The statistical enquiry cycle (PPDAC) can be used in summary, comparison, and time-series investigations. A comparison investigation compares similarities and differences for a variable across two or more groups, and a time-series investigation considers how a variable changes over time. Numerical variables can be counted or measured; discrete numerical variables are counted, continuous numerical variables are measured. A conjecture or assertion involves thinking about what data will show before it is collected or analysed. Data is not always accurately recorded; it needs to be checked for errors and may need correcting. Alternative data visualisations for the same data can lead to different insights.

Probability | Tūponotanga

By the end of this phase, students know that the statistical enquiry cycle (PPDAC) can be used for chance-based investigations. Probabilities and the language of probability are associated with values between 0 or 0% (impossible) and 1 or 100% (certain). They can be used to describe situations that involve uncertainty and help make decisions. In a chance-based investigation, the probability of an outcome is the relative frequency of the outcome in a probability experiment (the probability estimate). If outcomes are believed to be equally likely, the probability of an outcome is the number of times the outcome occurs divided by the total number of outcomes, where all possible outcomes can be listed (the theoretical probability).

Investigating situations | Te tūhura pūāhua

By the end of this phase, students can pose a question for investigation, find entry points for addressing the question, and plan an investigation pathway and follow it step by step. They can identify relevant prior knowledge, conditions, and relationships to support the investigation. They can monitor and evaluate progress, adjusting the investigation pathway if necessary, and make sense of outcomes or conclusions in light of a given situation and context.

Representing situations | Te whakaata pūāhua

By the end of this phase, students can use representations to find, compare, explore, simplify, illustrate, prove, and justify patterns and variations. They use representations to learn new ideas, explain ideas to others, investigate conjectures, and support arguments. They select, create, or adapt appropriate mental, oral, physical, virtual, graphical, or diagrammatic representations. They use visualisation to mentally represent and manipulate objects and ideas.

Connecting situations | Te tūhono pūāhua

By the end of this phase, students can suggest connections between concepts, ideas, approaches, and representations. They connect new ideas to things they already know. They also make connections with ideas in other learning areas and with familiar contexts.

Generalising findings | Te whakatauwhānui i ngā kitenga

By the end of this phase, students can notice and explore patterns, structure, and regularity and make conjectures about them. They identify relationships, including similarities, differences, and new connections. They represent specific instances and look for when conjectures about them might be applied in another situation or always be true. They test conjectures, using reasoning and counterexamples to decide if they are true or not. They use appropriate symbols to express generalisations.

Explaining and justifying findings | Te whakamārama me te parahau i ngā kitenga

By the end of this phase, students can make statements and give explanations inductively, based on observations or data. They make deductions based on knowledge, definitions, and rules. They critically reflect on others’ thinking, evaluating their logic and asking questions to clarify and understand. They use evidence, reasoning, and proofs to explain why they agree or disagree with statements. They develop collective understandings by sharing and building on ideas with others. They present reasoned explanations and arguments for an idea, solution, or process.

Teaching sequence

Expanding horizons of knowledge, and collaborating
Te whakawhānui i ngā pae o te mātauranga, me te mahi tahi

This section describes how the components of a comprehensive teaching and learning programme for the mathematics and statistics learning area are used during the second phase of learning at school.

Throughout phase 2, encourage students to see themselves as capable, confident, and competent mathematics and statistics thinkers whose ideas are valued, who treat mistakes as part of the learning process, and whose abilities in mathematics and statistics will develop over time with consistent effort. Confidence is built through experiencing success and developing competence and understanding. Over phase 2, students collaborate with others to expand their knowledge and understanding. Support this by working with the class to establish expectations and responsibilities for working together as peers, sharing thinking, and agreeing or disagreeing about mathematical and statistical learning.

Continuously monitor students’ cognitive load, reasoning, questions, and use of representations, and respond quickly to address any issues and misconceptions. Ensure teaching builds on what students already understand, know, and can do.

Explicit teaching

Use warm-up routines as a form of active recall that connects back to prior learning (e.g., quick challenges, curly questions, games). Plan for students to develop fluency through practice, using a range of approaches.
Use worked examples and break down new learning into clearly explained, manageable steps. Use mathematical and statistical symbols and notation conventions, explaining them and how they work. Teach conceptual understanding of number operations and efficient written and mental methods for them.
Connect mathematical and statistical learning within and across contexts. Teach connected procedures and concepts together (e.g., multiplication and division with area and volume). Make connections explicit by highlighting concepts students have applied in other learning areas.
Plan ways for students to consolidate their mathematical and statistical learning. Use prompts, questions, and situations that incorporate previously taught concepts and procedures, to help students retrieve and apply them. Highlight connections with new learning.

Positive relationships with mathematics and statistics

Encourage curiosity through exploring mathematics and statistics in, for example, history, games, art, and puzzles.
Highlight to the class the mathematical thinking and approaches of individuals or groups. Display drawings or photos of students’ representations and workings throughout the learning process, and use these to start conversations about mathematical and statistical learning and progress between students and with families.

Rich tasks

Plan to explore rich mathematical and statistical situations and contextual tasks that are useful and meaningful to the class or community.
Design tasks that use different contexts or combinations of operations to encourage students to apply their reasoning and knowledge to other types of problems (e.g., using decimals in measurement situations).
Encourage students to generalise by using questions such as “If I change this, what happens to that?” and “Is there another way to show this?”
Teach problem-solving and investigation strategies. Support students to read and make sense of a problem – through drawing, using materials, or trying some numbers – and then to identify relevant knowledge, plan how to solve the problem in a sequence of steps, take action to apply their plan (recording calculations with meaningful explanations), and check their findings.
Give students opportunities to notice and wonder about patterns, structures, and relationships and make statements about them.

Communication in mathematics and statistics

Plan for students to actively listen to, reflect, and build on each other’s thinking and learning. Use discourse-based tools and a range of open questions to facilitate productive discussions. Over the phase, encourage students to use evidence and examples to justify their claims and findings.
Select appropriate representations to show working and reasoning. Over the phase, move students towards using pictures, diagrams, and mathematical notation such as equations and inequalities. Teach students which representations are most effective for showing different types of information (e.g., number lines are important for representing operations, differences, the comparative size of numbers, and rounding conventions).
Prompt students to visualise and share their thinking about quantities, patterns, shapes, measurements, and data. Support students to visualise by estimating the number of items in a group, using rounding or known benchmarks to make estimations, and by noticing and responding to how a shape has been rotated or reflected, or is composed of other shapes.
Use mathematical and statistical language. Demonstrate the use of correct vocabulary that connects to the learning purpose or problem. Ask students to use correct vocabulary and to explain their findings and reasoning. In doing so, draw on students’ first and heritage languages, so that they can use their languages as a resource to connect their thinking and learning.
Dedicate time for students to record learning (e.g., in their mathematics and statistics book). Support them to organise their ideas clearly, using words, mathematical notation, and a range of representations. Provide opportunities for them to consider their goals and to reflect on their learning.

Number

	During year 4 Informed by prior learning, teach students to:	During year 5 Informed by prior learning, teach students to:	During year 6 Informed by prior learning, teach students to:	Teaching considerations
Number structure	skip count from any multiple of 100, forwards or backwards in 25s and 50s			Investigate patterns in multiples, using 100s boards or 1,000s books. Record choral counting on the board, and ask students to explain patterns and make generalisations or conjectures.
	identify, read, write, compare, and order whole numbers up to 10,000, and represent them using base 10 structure	identify, read, write, compare, and order whole numbers up to 100,000, and represent them using base 10 structure	identify, read, write, compare, and order whole numbers up to 1,000,000, and represent them using base 10 structure	Use marked number lines to order and compare numbers and place-value (PV) houses and materials to write and represent numbers, using base 10 structure. Support students to: practise saying, reading, and writing given numbers, including large numbers, using PV houses use PV houses to generalise that multiplying by 10 moves each digit in a number one place to the left, and dividing by 10 moves each digit one place to the right.
		identify factors of numbers up to 100	identify square numbers and factors of numbers up to 125	Represent factors of numbers using arrays or ordered lists of factor pairs. Use multiplication charts to investigate factors, multiples, and square numbers. Connect to students’ understanding of a square to explain and represent a square number and multiplication facts involving the same two numbers.
Operations	use rounding, estimation, and inverse operations to predict results and to check the reasonableness of calculations	use rounding, estimation, and inverse operations to predict results and to check the reasonableness of calculations	use rounding, estimation, and inverse operations to predict results and to check the reasonableness of calculations	Explain how to round numbers to an appropriate value to make an estimate for a calculation. Explain reasoning using estimation language such as ‘about’, ‘more or less', and ‘close to’. Connect rounding with: known benchmarks (e.g., doubles, halves, multiples of 10), to make estimations and check calculations rounding to an appropriate unit in measurement situations. Use number lines to support rounding, explaining how to find the midpoint between two numbers. Explain and justify findings by connecting to estimates and other checking methods. Use families of facts to show the connection between factors and multiples. Explain how to use families of facts to ‘work backwards’ (e.g., 7 × 8 = 56, so 56 ÷ 8 = 7).
	round whole numbers to the nearest thousand, hundred, or ten	round whole numbers to the nearest ten thousand, thousand, hundred, or ten, and round tenths to the nearest whole number	round whole numbers to a specified power of 10, and round tenths and hundredths to the nearest whole number or one decimal place
	add and subtract two- and three-digit numbers	add and subtract whole numbers up to 10,000	add and subtract any whole numbers	Explain and represent addition and subtraction using materials such as PV materials, number lines, and number discs. Explain and connect: the horizontal method and the vertical-column method of addition or subtraction making estimates or mental calculations using place value, partitioning, and known facts. Use worked examples and a range of problem types (e.g., result, change, start-unknown), using think-alouds to explain the most efficient approaches. Have students practise decoding and solving word problems, representing them as equations.
	recall multiplication and corresponding division facts for 4s and 6s	recall multiplication facts for 7s, 8s, and 9s and corresponding division facts	recall multiplication facts to at least 10 × 10 and corresponding division facts.	Provide a range of tasks for students to practise and develop fluency in new and previously learned multiplication and division facts (e.g., families of facts, multiplication table grids, arrays, games). Investigate patterns in the multiples of times tables and to generalise multiplication problems beyond recalled facts by looking for patterns.
	multiply a two-digit by one-digit number and two one-digit whole numbers (e.g., 23 × 5; 7 × 8)	multiply a three-digit by one-digit number and two two-digit whole numbers (e.g., 245 × 6; 34 × 83)	multiply multi-digit whole numbers (e.g., 54 × 112)	At year 4: connect multiplication with skip counting using jumps on a number line or arrays represent division using diagrams and equal sharing, connecting with known families of facts generalise the distributive property of multiplication over addition (e.g., 7 × 8 = 7 × (5 + 3) = (7 × 5) + (7 × 3). At years 5–6, represent multiplication using the area model, and make connections with place value (e.g., 34 × 7 = 30 × 7 + 4 × 7). Explain and demonstrate: the vertical-column method for division and multiplication, ensuring students understand and practise the procedure and connect with place value, known facts, and estimation making estimates or mental calculations by connecting to place value, partitioning, and known facts. Have students investigate: decoding and solving word problems, representing them as equations multiplication and division in measurement and proportional reasoning situations multiplication to count different combinations (e.g., “If I have 4 tops and 3 pairs of shorts, how many different outfits can I make?”)
	divide up to three-digit whole number by a one-digit divisor, with no remainder (e.g., 65 ÷ 5)	divide up to three-digit whole number by a one-digit divisor, with a remainder (e.g., 83 ÷ 5 = 16, remainder 3)	divide up to four-digit whole number by a one-digit divisor, with a remainder (e.g., 198 ÷ 7; 4154 ÷ 8)
			use the order of operations rule with grouping, addition, subtraction, multiplication, and division.	Use worked examples to demonstrate a step-by-step layout with one equal sign per line. Have students investigate: decoding and solving word problems, deciding which operation to use and why the distributive property of multiplication over addition and subtraction (e.g., 6 × 18 = 6 × (20 – 2) = (6 × 20) – (6 × 2). Explain the commutative, associative, and identity properties, and justify which operations they work for and which they don’t.
Rational numbers	identify, read, write, and represent tenths as fractions and decimals	identify, read, write, and represent tenths and hundredths as fractions and decimals	identify, read, write, and represent fractions, decimals (to two places), and related percentages	Represent and compare fractions, decimals, and percentages using continuous materials (double number lines, fraction walls, 100s squares). Have students practise saying, reading, and writing decimals using decimal PV houses. Explain and represent decimal tenths as a fraction with the denominator as 10, and percentages and decimals (to two places) as a fraction with the denominator of 100. Investigate situations where decimals are used (e.g., in measurements at a sports day).
	compare and order tenths as fractions and decimals, and convert decimal tenths to fractions (e.g., 0.3 =3—10)	compare and order tenths and hundredths as fractions and decimals, and convert decimal tenths and hundredths to fractions	compare and order fractions, decimals (to two places), and percentages, and convert decimals and percentages to fractions
	divide whole numbers by 10 to make decimals	divide whole numbers by 10 and 100 to make decimals	multiply and divide numbers by 10 and 100 to make decimals and whole numbers (e.g., 1.3 × 10 = 13)	Use decimal PV houses to generalise that multiplying by 10 moves each digit in a number one place to the left (increasing the place value of the digit), and dividing moves each digit one place to the right (decreasing the place value of the digit).
	for fractions with related denominators of 2, 4, and 8, 3 and 6, or 5 and 10: compare and order the fractions identify when two fractions are equivalent by directly comparing them, noticing the simplest form (e.g., 3—6 = 1—2 , which is the simplest form)	for fractions with denominators of 2, 3, 4, 5, 6, 8, 10, 12, or 100: compare and order the fractions identify when two fractions are equivalent	for fractions with denominators of 2, 3, 4, 5, 6, 8, 10, 12, or 100: compare and order the fractions identify when two fractions are equivalent represent the fractions in their simplest form	Use fraction walls (equivalence materials) to represent and investigate the relationship between the denominator and numerator in a fraction and how we can use this to simplify the fraction. Make connections with known facts such as halving and dividing by 4. Count forwards and backwards in fractions, and place fractions on marked and unmarked number lines.
	convert (using number lines) between mixed numbers and improper fractions with denominators of 2, 3, 4, 5, 6, 8, and 10	convert between mixed numbers and improper fractions with denominators of up to 10	convert between mixed numbers and improper fractions	Represent improper fractions using words and materials, and place them on a number line. At years 5–6, explain conversion as division with a remainder (e.g., 11—4 = 2 3—4 (11 divided by 4 = 2 r 3) or multiplication plus a remainder (e.g., 1 1—5 = 6—5 (1 × 5 + 1).
	find a unit fraction of a whole number, using multiplication or division facts and where the answer is a whole number (e.g., 1—5 of 40) identify, from a unit fraction part of a set, the whole set	find a fraction of a whole number, using multiplication and division facts and where the answer is a whole number (e.g., 2—3 of 24) identify, from a fractional part of a set, the whole set	find a fraction or percentage of a whole number where the answer is a whole number (e.g., 3—8 of 48; 30% of $150) identify, from a fractional part of a set, the whole set.	Use bar models, diagrams, or paper strips to represent equal parts of a whole. At year 4, represent parts of a whole set using discrete materials to make equal groups. At years 5–6, connect percentages and fractions of a whole to known facts and benchmarks (e.g., 25% and dividing by 4).
	add and subtract fractions with the same denominators to make up to one whole (e.g., 3—8 + 3—8 + 2—8 = 8—8 = 1)	add and subtract fractions with the same denominators, including to make more than one whole.	add and subtract fractions with the same or related denominators (e.g., 1—4 + 1—8)	Represent the addition and subtraction of fractions using fraction walls, number lines, and equations. At years 4–5, explain that, when adding and subtracting fractions with the same denominator, the numerators are added or subtracted but the denominator stays the same. At year 6, explain how to use equivalent fractions to rename fractions so that they all have the same denominator. Then add or subtract the numerators.
	add and subtract decimals to one decimal place (e.g., 1.3 + 0.2 = 1.5)	add and subtract whole numbers and decimals to two decimal places (e.g., 32.55 – 21.21 = 11.34)	add and subtract whole numbers and decimals to two decimal places (e.g., 250.11 + 135.29 = 385.4)	Explain and demonstrate both the horizontal method for representing an equation and the vertical-column method for addition or subtraction. Investigate and connect the addition and subtraction of decimals in measurement situations. At year 4, use number lines and decimals to add and subtract tenths, connecting tenths as fractions with tenths as decimals. At years 5–6, connect to methods of adding and subtracting whole numbers.
	use doubling or halving to scale a quantity (e.g., to double or half a recipe)	use known multiplication facts to scale a quantity	use known multiplication and division facts to scale a quantity	Represent multiplicative relationships using diagrams, materials, and bar models. Use problems such as “If this recipe feeds 4 people, how much of each ingredient do we need to feed 20 people”?
Financial mathematics	make amounts of money using dollars and cents (e.g., to make 3 dollars and 70 cents)	represent money values in multiple ways using notes and coins	solve problems involving purchases (e.g., ensuring they have enough money) create simple financial plans (e.g., shopping lists, a family budget)	Have students practise grouping denominations and making amounts using play money, connecting with place value, skip counting, and multiplication. Investigate authentic financial situations and represent findings using equations, spreadsheets, and tables.
Financial mathematics	estimate and calculate the total cost and change for items costing whole-dollar amounts.	estimate to the nearest dollar and calculate the total cost of items costing dollars and cents, and the change from the nearest ten dollars.	calculate 10%, 25%, and 50% of whole-dollar amounts (e.g., 50% of $280).	Investigate practical situations involving calculating costs and giving change. At year 6: use bar models to represent percentages of whole-dollar amounts, and connect to equivalent fractions explain the procedure of dividing a whole by 10 to find 10%, 2 to find 50%, or 4 to find 25%.

Algebra

	During year 4 Informed by prior learning, teach students to:	During year 5 Informed by prior learning, teach students to:	During year 6 Informed by prior learning, teach students to:	Teaching considerations
Equations and relationships	form and solve true or false number sentences and open number sentences involving multiplication and division, using an understanding of the equal sign e.g., 5 × __ = 20; __ ÷ 3 = 6)	form and solve true or false number sentences and open number sentences involving all four operations (e.g., 674 + 56 – __ = 671)	form and solve true or false number sentences and open number sentences involving all four operations, using an understanding of equality or inequality (e.g., 8 × 7 < 8 × 5 + 8 (T or F?)	Represent the equal sign as ‘the same as’ to demonstrate it is a symbol of equivalence. Explain the difference between an expression (e.g., 4 × 5), an equation (e.g., 4 × 5 = 20), and an inequality (e.g., 4 × 5 < 4 × 6). Have students practise the use of equal and inequality symbols. Investigate inverse operations to find missing numbers in equations.
Equations and relationships	recognise and describe the rule for a growing pattern using words, tables, and diagrams, and make conjectures about further elements in the pattern	use tables to recognise the relationship between the ordinal position and its corresponding element in a growing pattern, develop a rule for the pattern in words, and make conjectures about further elements or terms in the pattern	use tables, XY graphs, and diagrams to recognise relationships in a linear pattern, develop a rule for the pattern in words (i.e., that there is a constant amount of change between consecutive elements or terms), and make conjectures about further elements in the pattern	Explain vocabulary in relation to patterns (e.g., ordinal, element, term, position, rule) and how to record the position and term for each element in a pattern. Investigate visual patterns (e.g., tivaevae), making block patterns and representing patterns using pictures and materials.
Algorithmic thinking	create and use an algorithm for generating a pattern or pathway.	create and use an algorithm for generating a pattern, procedure, or pathway.	create and use algorithms for making decisions that involve clear choices.	Represent a procedure as a sequence of step-by-step instructions (an algorithm). Follow the sequence by ‘acting it out’, asking students to describe and record each step. Investigate giving directions for, or describing, the most efficient pathway on a maze or map, and sorting numbers according to a set of instructions (e.g., “Sort the odd numbers ... the multiples of 5”). Explain and justify how a procedure has been broken into steps, the order of the steps, whether there were any errors or omissions, and, if so, how they were corrected. At years 4–5, investigate creating a sequence of instructions (e.g., to draw a polygon or move through a maze), using digital tools or on paper. Connect with geometry when giving directions or describing pathways. At year 5, connect algorithmic thinking to a procedure for an operation (e.g., for multiplying two numbers). At years 5–6, investigate identifying the transformations used to create geometric patterns. At year 6, investigate using classification diagrams to identify an object, a shape, or data based on multiple characteristics.

Measurement

	During year 4 Informed by prior learning, teach students to:	During year 5 Informed by prior learning, teach students to:	During year 6 Informed by prior learning, teach students to:	Teaching considerations
Measuring	measure body parts (e.g., the arm) or familiar objects and use these as benchmarks to estimate and then measure length, mass (weight), capacity, and duration, using appropriate metric or time-based units	estimate and then accurately measure length, mass (weight), capacity, temperature, and duration, using appropriate metric or time-based units or a combination of units	estimate and then accurately measure length, mass (weight), capacity, temperature, and duration, using appropriate metric or time-based units or a combination of units	Investigate practical measuring situations, and have students practise the accurate use and reading of rulers, scales, timers, thermometers, and measuring jugs. Explain and accurately measure: at year 4, centimetres, metres, grams, kilograms, and litres, connecting with half units (e.g., 500 mL = 0.5 L) at years 5–6, centimetres, metres, millimetres, grams, kilograms, litres, millilitres, and degrees Celsius. Connect reading a measuring tool with rounding to the nearest given unit (e.g., 3.6 cm to the nearest cm). Discuss the meaning of measurements in context. Explain benchmarks and prompt students to develop them (e.g., “A big step is about a metre, so roughly how long is our classroom?”)
	use appropriate units to describe length, mass (weight), capacity, and time	use the appropriate tool for a measurement and the appropriate unit for the attribute being measured	select and use the appropriate tool for a measurement and the appropriate unit for the attribute being measured	Explain and justify the use of appropriate metric units or tools for measuring a given attribute with the precision necessary for the problem, noting that using smaller units provides more accuracy.
	use the metric measurement system to explore relationships between units	use the metric measurement system to explore relationships between units, including relationships represented by benchmark fractions and decimals	convert between common metric units for length, mass (weight), and capacity, and use decimals to express parts of wholes in measurements	Explain measurement prefixes (e.g., milli-, centi-), how they connect metric units, and how they are based on powers of ten and relate to place value. Investigate how measures can be partitioned and combined like other numbers, and how smaller units are created by equally partitioning larger units.
	recognise that angles can be measured in degrees, using 90, 180, and 360 degrees as benchmarks	describe angles using the terms acute, right, obtuse, straight, and reflex, comparing them with benchmarks of 90, 180, and 360 degrees	visualise, measure, and draw (to the nearest degree) the amount of turn in angles up to 360 degrees	Investigate different angles using physical and digital tools and angles in the environment, and comparing and classifying them as acute, right, reflex, or obtuse. Make connections between angles, fractions of a circle, and turns. At year 6, explain, demonstrate, and have students practise estimating angles and measuring and drawing them using a protractor.
	tell the time to the nearest 5 minutes, using the language of ‘minutes past the hour’ and ‘to the hour’	describe the differences in duration between units of time (e.g., days and weeks, months, and years), and solve duration-of-time problems involving 'am' and 'pm' notation	convert between units of time and solve duration-of-time problems, in both 12- and 24-hour time systems	Represent time using: digital and analogue clocks (at year 4), to practise telling the time analogue and digital forms (e.g., “It’s 12:45, or a quarter to one.”) Investigate using calendars, timetables, schedules, and number lines to work out the time between two events or the duration of an event. Explore solar calendars (e.g., Roman, Gregorian) and lunar calendars (e.g., maramataka Māori, Chinese). Explain subtracting for duration and inclusive counting (e.g., “For the number of days between now and next Tuesday, start counting from today”). Explain relationships between the units of time (e.g., 60 seconds to the minute, 60 minutes to the hour, 24 hours in a day, 365 days in a year), and use them to convert between units of time.
Perimeter, area, and volume	visualise, estimate, and measure: the perimeter of polygons, using metric units (cm and m) the area of shapes covered with squares or half squares the volume of shapes filled with centicubes, taking note of layers and stacking.	visualise, estimate, and calculate: the perimeter of regular polygons (in m, cm, and mm) the area of shapes covered with squares or partial squares the volume of rectangular prisms filled with centicubes, taking note of layers and stacking.	visualise, estimate, and calculate the area of rectangles and right-angled triangles (in cm² and m²) and the volume of rectangular prisms (in cm³), by applying multiplication.	Investigate practical measuring situations and connect: finding area with multiplication arrays finding area and volume with the commutative property of multiplication how part-units can be combined using number concepts, when finding the area of a shape the area of a right-angled triangle with half the area of a square. Have students represent written methods for calculating, with clearly laid-out working.

Geometry

	During year 4 Informed by prior learning, teach students to:	During year 5 Informed by prior learning, teach students to:	During year 6 Informed by prior learning, teach students to:	Teaching considerations
Shapes	identify, classify, and describe the attributes of polygons (including triangles and quadrilaterals) using properties of shapes, including line and rotational symmetry	identify, classify, and describe the attributes of: regular and irregular polygons, using edges, vertices, and angles prisms, using cross sections, faces, edges, and vertices	identify, classify, and explain similarities and differences between: 2D shapes, including different types of triangle prisms and pyramids	Use a range of 2D and 3D shapes, including tactile shapes, diagrams, student-made constructions, and digital shapes. Investigate line and rotational symmetry using mirrors and tracing paper. Connect to algorithmic thinking by making classification diagrams for classifying shapes.
Shapes	compare angles in 2D shapes, classifying them as equal to, smaller than, or larger than a right angle	identify and describe parallel and perpendicular lines, including those forming the sides of polygons	identify and describe the interior angles of triangles and quadrilaterals	Investigate interior angles using digital tools and paper shapes to generalise that the interior angles of a triangle add to 180° and those of a quadrilateral add to 360°. Connect these understandings to ideas about right angles, straight lines, and full turns.
Spatial reasoning	identify the 2D shapes that compose 3D shapes (e.g., a triangular prism is made from two triangles and three rectangles)	visualise 3D shapes and connect them with nets, 2D diagrams, verbal descriptions, and the same shapes drawn from different perspectives	visualise and draw nets for rectangular prisms	Represent 3D shapes using digital tools, sketches, blocks, and student-made constructions. Investigate nets that will or will not fold, and match solid shapes with nets.
Spatial reasoning	visualise, predict, and identify which shape is a reflection, rotation, or translation of a given 2D shape	resize (enlarge or reduce) a 2D shape	visualise, create, and describe 2D geometric patterns and tessellations, using rotation, reflection, and translation and identifying the properties of shapes that do not change	Investigate using 2D shapes, squared paper, mirrors, and tracing paper to make and test conjectures about the effects of transformations. At year 5, use a grid to scale a shape and connect the scaling with multiplication or division. At year 6, generalise the properties of shapes that do not change when transformed (e.g., “Which properties of a square stay the same when we rotate it 90 degrees?”)
Pathways	use grid references to identify regions and plot positions on a grid map interpret and describe pathways, including those involving half and quarter turns and the distance travelled.	interpret and create grid maps to plot positions and pathways, using grid references and directional language, including the four main compass points.	interpret and create grid references and simple scales on maps use directional language, including the four main compass points, turn (in degrees), and distance (in m, km) to locate and describe positions and pathways.	Investigate different types of maps (e.g., schematic, topographical, and digital maps). Explain pathways using directional language, including te reo Māori (e.g., whakamua/forwards, whakamuri/backwards, whakamauī/to the left, whakamatau/to the right, raki/north, tonga/south, rāwhiti/east, uru/west). Connect compass points and directional language with turns and angles, and simple scales with proportional reasoning.

Statistics

	During year 4 Informed by prior learning, teach students to:	During year 5 Informed by prior learning, teach students to:	During year 6 Informed by prior learning, teach students to:	Teaching considerations
Problem	use multivariate data to investigate summary and comparison situations with categorical and discrete numerical data, by: posing an investigative question that can be answered with data making conjectures or assertions about expected findings		use multivariate data to investigate summary, comparison, and time-series situations, by: posing an investigative question that can be answered with data making conjectures or assertions about expected findings	Show, with student input, how to: pose summary and comparison investigative questions pose time-series investigative questions (at year 6). Connect questions to areas of interest and value to the students and their communities.
Plan	plan how to collect primary data to support answering the investigative question, including: deciding on the group of interest deciding on the variable or variables for which data will be collected taking account of ethical practices in data collection		plan how to collect primary data or how to use provided data, including identifying the variables of interest and, for provided data: identifying who the data was collected from identifying the original investigator’s purpose for collecting the data deciding if the source is reliable (e.g., by checking if survey questions appear to be biased towards a particular point of view)	Show, with student input, how to: ask interrogative questions about sources and ethical practices develop and closely examine survey or data-collection questions define or establish measures for variables identify ‘who, what, where, when, and how’ when using secondary datasets.
Data	use a variety of tools to collect the data, and check for errors in it	use a variety of tools to collect the data, check for errors in it, and correct them by re-collecting the data, if possible	collect primary data and check for errors, and provide information about variables in secondary data (e.g., how data was collected for them and possible outcomes for them)	Show, with student input, how to: use a range of representations for recording data identify what errors in data look like. Connect multiple variables for individuals, explaining that most datasets use a table design in which each row focuses on an individual and each column includes the data on multiple individuals for one variable.
Analysis	create and describe data visualisations to make meaning from the data, with statements including the name of the variable	create and describe data visualisations to make meaning from the data, with statements including the names of the variable and group of interest	create and describe a variety of data visualisations to make meaning from the data, identifying features, patterns, and trends in context, and including the variable and group of interest	Show, with student input, how to: represent and analyse data visualisations, creating them at first by hand and then with digital tools identify the different features of data that the data visualisation reveals and how to describe them read the data, and read ‘between’ the data. Explain how different data visualisations have different features and how to describe them in context (e.g., in relation to frequency, modes, modal groups, patterns, trends, values for numerical variables).
Conclusion	choose descriptive statements that best answer the investigative question, reflecting on findings and how they compare with initial conjectures or assertions	answer the investigative question, comparing findings with initial conjectures or assertions and their existing knowledge of the world		Show, with student input, how to: choose the best descriptive statements that answer an investigative question prepare their findings and explain them to others.
Statistical literacy	check the statements that others make about data to see if they make sense, using information to clarify or correct statements where needed.	check and, if necessary, improve the statements others make about data, including data from two or more sources.	identify, explain, check, and, if necessary, improve features in others' data investigations (e.g., biased survey questions, misleading information or statements).	Show, with student input, how to: identify misleading data visualisations, match others’ data visualisations with their statements, and check the claims made by others interpret pie graphs (but not how to create them) explain and justify the effectiveness of data visualisations in representing others’ findings, using interrogative questions.

Probability

During year 4
Informed by prior learning, teach students to:

During year 5
Informed by prior learning, teach students to:

During year 6
Informed by prior learning, teach students to:

Teaching considerations

Probability investigations

engage in chance-based investigations with equally likely outcomes by:
- posing an investigative question
- anticipating and then identifying possible outcomes for the investigative question
- generating all possible ways to get each outcome (a theoretical approach), or undertaking a probability experiment and recording the occurrences of each outcome
- creating data visualisations for possible outcomes
- describing what these visualisations show
- finding probabilities as fractions
- answering the investigative question
- reflecting on anticipated outcomes

engage in chance-based investigations, including those with not equally likely outcomes, by:
- posing an investigative question
- anticipating and then identifying possible outcomes for the investigative question
- generating all possible ways to get each outcome (a theoretical approach), or undertaking a probability experiment and recording the occurrences of each outcome
- creating data visualisations for possible outcomes
- describing what these visualisations show
- finding probabilities as fractions
- answering the investigative question
- reflecting on anticipated outcomes
- (at year 6) comparing findings from the probability experiment and associated theoretical probabilities, if the theoretical model exists

Investigate everyday chance-based situations in order to explore and experience the chance, randomness, variation, and distribution of outcomes.

Use digital tools to conduct a large number of trials in order to see what a probability estimate and probability distributions look like.

Support students to represent:

probability outcomes (theoretical and experimental) using lists, tables, tally charts, visualisations of distributions, words, and numbers
the chance of an outcome occurring using fractions, decimals, and percentages.

Connect investigative questions to outcomes and with all possible ways to get the outcomes.

Connect anticipated outcomes with theoretical and experimental distributions.

Critical thinking in probability

agree or disagree with others’ conclusions about chance-based investigations.

evaluate others’ statements about chance-based investigations, with justification.

identify, explain, and check others’ statements about chance-based investigations, referring to evidence.

Show, with student input, how to:

match the results of chance-based investigations with statements, and check the claims in others’ investigations
explain and justify the statements made by others about chance-based investigations, using interrogative questions.

The language of mathematics and statistics: Phase 2

	Year 4 Students will know the following words:	Year 5 Students will know the following words:	Year 6 Students will know the following words:
Number	addend convert decimal decimal place decimal point improper fraction mixed number rename scale tenth	change divisor, dividend, quotient, remainder factor hundredth multiple product proportion	efficient inverse operation percentage simplest form square number thousandth
Algebra	conjecture relationship	algorithm corresponding element procedure	constant equality, inequality linear pattern XY graph
Measurement	angle benchmark degree kilogram minutes past, minutes to	a.m., p.m. acute angle attribute degrees celsius kilometre, millimetre obtuse, reflex, right, or straight angle timetable	cubic centimetre, cubic metre protractor square centimetre, square metre
Geometry	grid reference rotational symmetry	compass points cross section net parallel or perpendicular line perspective prism regular or irregular polygon resize, enlarge, reduce	centre of rotation clockwise, anticlockwise interior angle map scale right-angled, equilateral, isosceles, or scalene triangle tessellation
Statistics	analysis assertion investigative question conclusion	categorical data visualisation discrete numerical group of interest source	comparison or summary investigative question feature misleading mode primary or secondary data trend
Probability	chance-based investigation equally likely outcome probability experiment	evaluate not an equally likely outcome	evidence

Mathematics and Statistics Learning Area Years 0–8 glossary

Abstract	Symbolic representation of a concept.
Acceleration	Acceleration or accelerated learning is where students are enabled to learn concepts and procedures more rapidly than the expected rate of progress. Accelerated learning approaches involve teaching students year-level content and experiences and supporting them with appropriate scaffolds to make this work accessible.
Additive identity	Zero will not change the value when added to a number. For example, 16 + 0 = 16.
Algorithm	A set of step-by-step instructions to complete a task or solve a problem.
Algorithmic thinking	Defining a sequence of clear steps to solve a problem.
Argument	Providing an idea or finding that is based on reasoning and evidence.
Associative property	A property of operations when three numbers can be calculated (addition or multiplication) in any order without changing the result. For example, (4 + 3) + 7 = 4 + (3 + 7) because 7 + 7 = 4 + 10, and (4 x 3) x 5 = 4 x (3 x 5).
Assumptions	A proposition (a statement or assertion) which is taken as being true with respect to a given context.
Attribute	A characteristic or feature of an object or common feature of a group of objects —such as size, shape, colour, number of sides.
Base 10	Our number value system with ten digit symbols (0-9); the place value of a digit in a number depends on its position; as we move to the left, each column is worth ten times more, with zero used as a placeholder; to the right, the system continues past the ones’ column, to create decimals (tenths, hundredths, thousandths); the decimal point marks the column immediately to the right as the tenths column.
Benchmarks	A reference point that we can use for comparison or estimation. For example, “My finger is about one centimetre wide.”
Categorical variables	A variable that classifies objects or individuals into groups or categories. For example, hair colour, breed of dog.
Chance	The likelihood that an outcome will occur.
Claim	A statement of what the student believes to be correct.
Commutative property	In addition and multiplication, each number can be operated in any order. For example, 5 + 6 = 6 + 5.
Compose and decompose	Compose is to make a shape using other shapes. Decompose is to break a shape into other shapes.
Comparison investigative question	An investigative question that compares a variable across two clearly identified populations or groups. For example, “I wonder if girls in our class tend to be taller than boys in our class?”
Conceptual understanding	The comprehension of mathematical concepts, operations, and relations by connecting related ideas, representing concepts in different ways, identifying commonalities and differences between aspects of content, communicating their mathematical thinking, and interpreting mathematical information.
Conjecture	A statement whose truth or otherwise is not yet determined but is open to further investigation.
Constant	A constant term is a fixed value that will not change.
Continuous materials	Models based on relative length or area, such as a number line, fraction wall, bar model.
Data	A collection of facts, numbers, or information; the individual values of which are often the results of an experiment or observations.
Data ethics	The principles behind how data is gathered, protected, and used; at the core of ethical practice is the need to do good and to do no harm.
Data visualisations	A graphical, tabular, or pictorial representation of information or data.
Deduction	Make a conclusion based on knowledge, definitions, and rules.
Digital tools	Digital applications, calculators.
Discrete materials	Separate objects that can be counted and grouped. For example, counters, ice block sticks.
Discrete numerical variables	Variables that can be counted and have a limited range of possibilities. For example, number of students in each team, the result of rolling a die.
Disinformation	False information spread deliberately to deceive others.
Distribution	In mathematics, distribution describes spreading terms out equally across an expression; in statistics, distribution describes how data values are spread across the range of values collected.
Distributive property	An operation is said to be distributive over another operation if it can take priority over the operation used for combination within brackets. For example, 6 × 17 = 6 × (10 + 7) = (6 × 10) + (6 × 7) = 60 + 42 = 102.
Efficient	A procedure is said to be efficient when it is carried out in the most simple and effective way.
Element in a pattern	In a repeating pattern, an element is the repeating core. In a growing pattern, an element is a section of the pattern. For example, in the Fibonacci sequence 1, 1, 2, 3, 5, 8, the next element is the sum of the previous two elements (5 + 8 = 13).
Equation	A number statement that contains an equal sign. The expressions on either side of the equal sign have the same value (are equal).
Equivalent fraction	Two different fractions that represent the same number are referred to as equivalent fractions. For example, 1—2, 2—4, 3—6, and 4—8 are equivalent fractions because they represent the same number.
Estimate	A rough judgement of quantity, value, or number. In statistics, an assessment of the value of an existing, but unknown, quantity. In probability, the probability of an outcome in an experiment.
Event	One or more outcomes from a probability activity, situation, or experiment.
Evidence	Information, findings, data that support (prove) a statement or argument.
Expression	Two or more numbers, operations or variables connected by operations. Expressions do not include an equal or inequality sign.
Families of facts	A group of equations that use the same numbers. For example, 3 x 2 = 6, 2 x 3 = 6, 6 ÷3 = 2, 6 ÷ 2 = 3.
Generalisation	To recognise and describe patterns in relationships.
Growing pattern	A pattern where there is a constant increase or decrease between each term. For example, 5, 10, 15, 20.
Horizontal method	Representing the operation as an equation across the page, often partitioning one of the numbers into tens and units. For example, 16 + 23 = 16 + 20 + 3.
Inequality	A statement in which one number or expression is greater or less than another.
Inference	Making a conclusion based on evidence and reasoning.
Informal unit	A non-standard unit used to measure. For example, blocks, pens, fingers. The informal units used should all be the same size.
Interpret	To make meaning from something.
Inverse operations	The opposite operation, so addition is inverse to subtraction, and multiplication is inverse to division. They are useful to check calculations. For example, to check 4 x 5 = 20, we can see if 20 ÷5 = 4.
Limitations	Possible missing evidence or information.
Mathematical modelling	An investigation of the relationships and behaviours of quantities in physical, economic, social, and everyday contexts; used to analyse applied situations and make informed decisions, starting the model with forming assumptions.
Misconception	A misunderstanding about a procedure, method or definition in mathematics or statistics. This could be about which procedure is needed, how the procedure or method should be followed or an incorrect definition. For example, thinking that 2.5 is the decimal form of 2/5.
Misinformation	Incorrect information (mistakes).
Multiplicative identity	When a number is multiplied by 1, it does not change its value. For example, 15 x 1 = 15.
Number sentence	An equation or inequality expressed using numbers and mathematical symbols. For example, 10 = 3 + 7 + 5 + 5.
One step transformation	One change in a shape's position or size. For example, a triangle is flipped (reflected).
Ordinal	The numerical position of the element in the sequence. For example, first, second, third.
Orientation	The angle that an object is positioned.
Outcomes	A possible result of a trial of a probability activity or a situation involving an element of chance; could also refer to a result or a finding.
Partition and regroup	Partitioning is the process of "breaking up" numbers. For example, 55 = 50 + 5. Regroup means to rearrange the formation of the group. For example, 55 = 40 + 15 or 55 = 30 + 25.
Primary data	Data collected first-hand for a specific purpose. For example, a survey, experiment, or interview.
Probabilistic thinking	Considering the likelihood (chance) of an outcome occurring; this is based on logic and reasoning.
Probability experiment	A test that can be carried out multiple times in the same way (trials). The outcome of each trial is recorded.
Procedural fluency	Choosing procedures appropriately and carrying them out flexibly, accurately, and efficiently. It is not the same as memorisation of facts and steps; rather it is being able to activate what you know and when to use it.
Procedure	A sequence of operations carried out in a specific order, such as the procedure to multiply two numbers, or the procedure to measure an object.
Quantifying	Expressing a quantity using numbers.
Rational number	All integers, fractions, and decimals.
Reasoning	Analysing a situation and thinking and working mathematically to arrive at a finding. Inductive reasoning is where an explanation is made based on observations and data. For example, “18 out of 22 people in our class like grapes, so grapes are the favourite fruit of our class.” Deductive reasoning is where we apply a known rule or fact to solve a problem. For example, prime numbers have two factors (itself and one), 4 has three factors, so it is not a prime number.
Relational	Symbols that show relationships between elements (terms) in an expression. For example, =, <, >
Repeating pattern	A pattern containing a 'unit of repeat'. For example, red, green, blue, red, green, blue.
Secondary data	Data collected by someone else, or a process, and/or obtained from another source. For example, online, books, other researchers.
Subitise	Instantly recognise the number of items in an arrangement without counting.
Summary investigative question	A question that asks about the overall distribution of the data or what is typical and reflects the population or group. For example, “I wonder how many pets are in our class? I wonder what the heights of the students in the class are?”
Tangible and intangible	Tangible is an object that can be touched. For example, a group of blocks. Intangible is a quality or measurement that cannot be touched. For example, colour or length.
Term in a pattern	One of the numbers in a pattern or sequence. For example, for 2, 4, 6, 8, the second term is 4.
Theoretical probability	A calculation of how likely an event is to occur in a situation involving chance.
Uncertainty	In probability, when the chance of an event occurring is unknown.
Unit of repeat	The part of a repeating pattern that repeats. The part is made up of several elements
Variables (statistics and algebra)	A property that may have different values for different individuals (statistics) or that may have different values at different times (statistics and algebra).
Variation	The differences seen in the values of a property for different individuals or at different times.
Vertical column method	The method for solving an operation by recording numbers in columns according to place value, working down the page.
Visualisation	To mentally represent and manipulate.

NZC - Mathematics and statistics (Phase 2)

Tags

Page quick links

About this resource

Progress outcome by the end of year 6

Teaching sequence

Explicit teaching

Positive relationships with mathematics and statistics

Rich tasks

Communication in mathematics and statistics

Number

Algebra

Measurement

Geometry

Statistics

Probability

The language of mathematics and statistics: Phase 2