NZC - Mathematics and statistics (Phase 1)

Progress outcome and teaching sequence for Phase 1 (year 0-3) of the Mathematics and statistics Learning Area. From 1 January 2025 this content is part of the statement of official policy relating to teaching, learning, and assessment of Mathematics and statistics in all English medium state and state-integrated schools in New Zealand.

NZC – Mathematics and statistics

Years 0‑8

NZC – Mathematics and statistics

Phase 1 – Years 0‑3

NZC – Mathematics and statistics

Phase 2 – Years 4‑6

NZC – Mathematics and statistics

Phase 3 – Years 7‑8

Page quick links

Mathematics and statistics: Phase 1 (Years 0-3)

Progress outcome by the end of year 3 (Foundation)

Teaching sequence – Phase 1 (Years 0-3)

About this resource

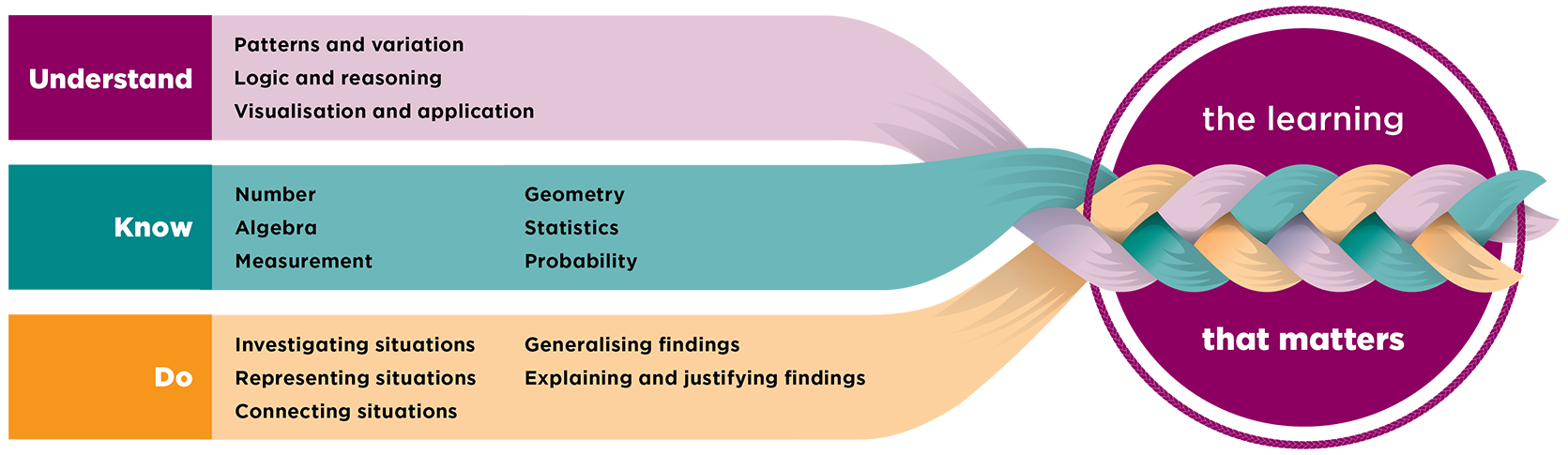
This page provides the progress outcome and teaching sequence for Phase 1 (Year 0-3) of the Mathematics and statistics learning area of the New Zealand Curriculum, the official document that sets the direction for teaching, learning, and assessment in all English medium state and state-integrated schools in New Zealand. In mathematics and statistics, students explore relationships in quantities, space, and data and learn to express these relationships in ways that help them to make sense of the world around them. Other parts of the learning area are provided on companion pages.

We have also provided the Maths Years 0-8 curriculum in PDF format. There are different versions available for printing (spreads), viewing online (single page), and to view by phase. You can access these using the icons below. Use your mouse and hover over each icon to see the document description.

Reviews

Te Mātaiaho | The New Zealand Curriculum

Mathematics and statistics: Phase 1 – Years 0‑3

Thriving in environments rich in literacy and maths
Te tupu pāhautea i te taiao ako e haumako ana i te reo matatini me te pāngarau

Progress outcome by the end of year 3 (Foundation)

The critical focus of phase 1 is for all students to thrive in environments rich in literacy and maths. In mathematics and statistics, students learn to use logic and reasoning to investigate, classify, and describe patterns and variations in quantities, shapes, and data. They begin to generalise and to understand the properties of numbers and attributes of shapes. They use materials, number lines, and pictures to visualise these concepts, make connections between representations, and explain their reasoning.

The phase 1 progress outcome describes the understanding, knowledge, and processes that students have multiple opportunities to develop over the phase.

The phase 1 progress outcome is found in the table below.

Understand

As students build knowledge through their use of the mathematical and statistical processes, they begin to understand the following.

Patterns and variation | Ngā ia auau me ngā rerekētanga

The world is full of patterns and is defined by a multitude of relationships in which change and variation occur. Mathematics and statistics provide structures that are useful for noticing, exploring, and describing different types of patterns and relationships, enabling us to generate insights or make conjectures.

Logic and reasoning | Te whakaaro arorau me te whakaaroaro

By engaging with mathematical concepts, we develop logical reasoning and critical thinking skills that enable us to evaluate information, question assumptions, and present arguments with clarity. Statistical reasoning from observation and theory allows us to differentiate what is probable from what is possible and to draw reliable conclusions about what is reasonable.

Visualisation and application | Te whakakite me te whakatinana

The visualisation of mathematical and statistical ideas profoundly influences how we perceive, understand, and interact with abstract concepts. Application in mathematics and statistics involves creating structures and processes that help us understand complex situations, enabling better decision making and communication of ideas.

Know

Number | Mātauranga tau

By the end of this phase, students know that our number system is base 10, with ten digit symbols. The place value of a digit in a number depends on its position; as we move to the left, each column is worth ten times more, with zero used as a placeholder. Students know that they can subitise (recognise without counting) patterns to support estimations and calculations. They know that numbers can be partitioned and recombined in different ways. Addition is putting parts together to find a total or whole. Subtraction takes parts away from a whole; it is also the difference between numbers. Multiplication and division involve recognising and working with equal groups and how many are in each group, the number of groups, and the total amount.

Students come to know that fractions are numbers that can be represented using words, pictures, or symbols. When fractions are represented symbolically, the bottom number (the denominator) shows how many pieces a whole has been equally split into, and the top number (the numerator) shows how many of those parts the fraction represents. Fractions show parts of a whole region, set of objects, or measurement.

Algebra | Taurangi

By the end of this phase, students know that patterns are made up of elements, including numeric or spatial elements, in a sequence governed by a rule. Repeating patterns have a unit of repeat; growing patterns can increase or decrease. The equal sign is relational in that it shows that the two sides of an equation represent the same quantity. Students also know that an algorithm is a set of step-by-step instructions for completing a task or solving a problem.

Measurement | Ine

By the end of this phase, students know that systems of measurement have a history and that different cultures use different approaches to measuring. Students know that they can measure and compare various attributes, such as length, area, volume, capacity, mass (weight), temperature, time, duration, and turn, using informal or standard units. When measuring, the measurement units must remain the same and there must be no gaps or overlaps between them. Students also know that the distance around the boundary of a two-dimensional shape gives perimeter, covering a surface gives area, and filling a three-dimensional shape gives capacity or volume.

Geometry | Āhuahanga

By the end of this phase, students know that patterns in shapes can be used to compare, classify, and predict. Two- and three-dimensional shapes have features that can be observed and described using geometric language. Shapes and objects can flip (reflect), turn (rotate), slide (translate), and be used to create patterns. Objects can be rotated in space and may appear different from other perspectives. Students know that maps are two-dimensional representations of places in the world with symbols to show locations and landmarks. The position of a location can be described relative to another location, including a known environmental feature.

Statistics | Tauanga

By the end of this phase, students know that data is information about the world, that it comes in many forms, and that it helps them to learn about people, their lives, and their environment. They know that a statistical enquiry cycle can be used to investigate a group, using questions that they ask of the data for the group. A variable refers to an attribute or measurement of the people or objects being studied, such as colour, height, or number of children. Sorting and organising the data for variables helps to make sense of data and to answer summary investigative questions. Data visualisations are representations of all available values for one or more variables that reveal relationships or tell a story.

Probability | Tūponotanga

By the end of this phase, students know that a chance-based situation has a set of possible outcomes that can be arranged into events. The probability of an event is the chance of it occurring.

Investigating situations | Te tūhura pūāhua

By the end of this phase, students can work with others to pose a question for investigation, find entry points for addressing the question, and plan an investigation pathway and follow it. They can identify relationships and relevant prior experience and knowledge to support the investigation. They can describe progress on the investigation pathway and work with others to make sense of outcomes or conclusions in the light of a given situation and context.

Representing situations | Te whakaata pūāhua

By the end of this phase, students can use representations to explore, find, and illustrate patterns. They use representations to learn new ideas and explain ideas to others, and they use visualisation to mentally represent and manipulate groups and shapes. They select or create appropriate mental, oral, physical, or virtual representations.

Connecting situations | Te tūhono pūāhua

By the end of this phase, students can suggest connections between concepts, ideas, approaches, and representations. They connect new ideas to things they already know. They also make connections with ideas in other learning areas and with familiar local contexts.

Generalising findings | Te whakatauwhānui i ngā kitenga

By the end of this phase, students can notice and explore patterns, structure, and regularity and make conjectures about them. They identify relationships, including similarities, differences, and new connections. They represent specific instances and look for when conjectures about them might be applied in another situation or always be true. They test conjectures, using reasoning and counterexamples to decide if they are true or not. They use words and pictures to express generalisations.

Explaining and justifying findings | Te whakamārama me te parahau i ngā kitenga

By the end of this phase, students can make statements and give explanations about what they notice and wonder, and they make deductions based on prior knowledge. They ask questions to clarify and understand others’ thinking and use evidence and reasoning to explain why they agree or disagree with statements. They develop collective understandings by sharing and building on ideas with others and can present basic explanations and arguments for an idea, solution, or process.

Teaching sequence – Phase 1 (Years 0-3)

Thriving in environments rich in literacy and maths
Te tupu pāhautea i te taiao ako e haumako ana i te reo matatini me te pāngarau

This section describes how the components of a comprehensive mathematics and statistics teaching and learning programme are used during the first phase of learning at school.

Throughout phase 1, students experience teaching that encourages curiosity and fosters success, as they explore environments and contexts rich in number and spatial elements. Active, hands-on experiences engage them in mathematics and statistics, with meaningful tasks that reflect their interests and the world outside the classroom.

Continuously monitor students’ reasoning, questions, engagement, and use of representations, and respond quickly to address any misconceptions. Be mindful of providing manageable learning experiences, building on students’ prior learning and leading to further challenge.

Explicit teaching

Engage students in the mathematical and statistical processes of Do. Explicitly teach students to use them, and demonstrate them regularly as part of the teaching.
Teach connected concepts and procedures together. For example, when teaching time (within the measurement strand) connect with fractions (within number) and turns (within geometry). Point out connections within concepts (e.g., “If I know 3 + 4, then I know 4 + 3”).
Demonstrate new concepts or procedures using clearly explained, manageable steps.
Think ‘aloud’. Voice decision making (e.g., about which numbers or operations to use) while demonstrating a procedure or process.
Ensure that every student engages in the active recall of previous learning (e.g., through games, matching activities, ‘think, pair, share’). Prompt students to make connections between previous and new learning.
Plan ways for students to consolidate their mathematical and statistical learning and build procedural fluency. Use a range of guided and independent practice tasks, such as working on problems that use a procedure that has been demonstrated. Use songs, games, materials, families of facts, and digital tools to build fluency and for students to practise skip counting, addition, subtraction, multiplication, and division facts.

Positive relationships with mathematics and statistics

Encourage students to ‘have a go’ and take risks. Reinforce the idea that mistakes help us learn as we try new procedures or share ideas.
Select highly interesting contexts based on knowledge of students’ personal experiences and backgrounds. Encourage students to connect with mathematics and statistics outside school by bringing in photos, resources, books, and other artefacts from home that link to mathematics and statistics learning.

Rich tasks

Use open-ended investigations with the whole class, groups, or individuals to support students to understand concepts and extend their learning. For example, plan investigations into local situations (e.g., “What should the new items on the lunch order menu cost?”) and into mathematical situations (e.g., the different ways of partitioning 24 into smaller groups).
Choose problems or investigations that help students notice structures and relationships (e.g., present and discuss ‘odd-one-out’ numbers or shapes).
Teach problem-solving and investigation strategies. Support students to read and make sense of a problem – through drawing, using materials, or trying some numbers – and to then plan how to solve it, take action to apply their plan, and check their findings.

Communication in mathematics and statistics

Use numbers, materials, and pictorial representations (e.g., diagrams and pictures). Select representations that support the purpose of learning and help students to show their thinking and reasoning and to learn new ideas. Over the phase, move students towards using symbols and showing operations as equations. Number lines are a key representation in this phase for showing, ordering, and comparing numbers (including fractions) and for demonstrating operations.
Prompt students to visualise and identify patterns, connections, and structures. Engage them in tasks where they are sorting, grouping, partitioning, and discussing what they have noticed and are wondering about. Guide them to notice and respond to patterns, similarities, and differences.
Build students’ mathematical and statistical vocabulary. Use games, songs, word walls, books, and digital tools. Intentionally use vocabulary to connect students’ informal language with appropriate mathematical and statistical language. In doing so, draw on students' first and heritage languages, so that they can use their languages as a resource to connect their thinking and learning.
Foster interactions that allow students to discuss, clarify, and explain their mathematical and statistical ideas. Encourage students to summarise, ask questions, and make suggestions. Help them to recall and connect mathematical and statistical learning using questions, materials, and verbal or visual prompts.

Number

	During the first 6 months Informed by prior learning, teach students to:	During the first year Informed by prior learning, teach students to:	During the second year Informed by prior learning, teach students to:	During the third year Informed by prior learning, teach students to:	Teaching considerations
Number structure	subitise (recognise without counting) the number of objects in a collection of up to 5	subitise (recognise without counting) the number of objects in a collection of up to 10, including by combining two patterns of 1–5 objects	group objects in a collection of at least 10, subitise the number of objects in each part, and find the total number in the collection using the parts	estimate the number of objects in a collection of less than 100, using patterns and groupings	Use a range of materials and images that represent structured and unstructured patterns and collections (e.g., dot patterns, 10s frames, dice, materials that can be grouped in 10 such as ice-block sticks). Also use language that quantifies and compares pattern arrangements (e.g. more, less, the same, different, combine, separate). Connect subitising to partitioning collections of objects (e.g., 6 and 2 on two dice are the same as 5 and 3 on two 10s frames).
	count forwards or backwards from any whole number between 1 and 10, and then between 1 and 20	count forwards or backwards in 1s, 2s, and 10s from any whole number between 1 and 20, and then between 1 and 100	count forwards or backwards in 1s, 2s, 5s, and 10s from any whole number between 1 and 100	count forwards or backwards in 2s, 3s, 5s, and 10s from any whole number between 1 and 1,000	Use a range of materials (e.g., number lines, 100s boards, number flip charts, 1,000s books, a Slavonic abacus, ice-block stick bundles). In general, support students to practise counting (e.g., in 2s and 5s) in short sequences (e.g., at year 3, “Count in 1s from 895 to 904; count in 2s from 90 to 110”). Investigate short patterns in multiples of 2s, 3s, 5s, and 10s, using rhymes, songs, choral counting, the grouping of discrete objects, the recording of patterns, and picture books. Have students practise finding 1, 10, or 100 more or less for a given number. Use materials to support students to identify numbers and patterns (e.g., 100s boards, 1,000s books). Connect to te reo Māori to support place-value (PV) understanding (e.g., tekau mā tahi (10 and 1), toru tekau mā rua (30 and 2).
	identify, read, and write whole numbers up to at least 10	identify, read, and write whole numbers up to at least 20, and represent them using the ten-and-ones structure of teen (11-19) and -ty (multiples of 10) numbers (e.g. 17 = 10 + 7, 20 = 2 × 10)	identify, read, and write whole numbers up to at least 100, and represent them using base 10 structure	identify, read, and write whole numbers up to at least 1,000, and represent them using base 10 structure	Have students practise saying, reading, and writing any given number within an identified number range. Use materials to support this (e.g., number flip boards, PV flip charts and houses). Explain that base 10 structure is based on groups of ten (ten ones form one ten, ten tens form one hundred, ten hundreds form one thousand etc.) and that both the position and value of a digit indicate the quantity it represents (e.g., 64 has 6 tens and 4 ones, 60 + 4 = 64). Have students investigate and represent the base 10 structure of numbers using a range of materials and digital tools (e.g., 100s boards, PV houses, PV blocks, ice-block sticks, arrow cards, number fans, words, numerals). Investigate odd and even numbers and the patterns they notice. Connect numerals, representations of them, and language (e.g., 652 represented with PV money: “652 = 600 + 50 + 2, 6 hundreds + 5 tens + 2 ones, six hundred and fifty two”).
	compare and order whole numbers up to at least 10 and ordinal numbers (e.g., 1st, 2nd, 3rd), using words	compare and order whole numbers up to at least 20 and ordinal numbers (e.g., 1st, 2nd, 3rd), using words or numerals and suffixes	compare and order whole numbers up to at least 100	compare and order whole numbers up to at least 1,000	Show the sequencing of numbers using a number line (select-numbered, marked, or empty). Change the number-line orientation from horizontal to vertical if students need support with the concepts of before and after. Explain and use the language of comparison when demonstrating why one number is larger or smaller than another (e.g., “63 is larger than 36, as 6 tens is larger than 3 tens”). Show how the position of digits in the PV structure helps us to order and compare two- and three-digit numbers.
	partition up to 5 objects, and then up to 10 objects, using a systematic approach and noticing patterns	partition and regroup up to 20 objects in different ways, using a systematic approach and noticing patterns	partition and regroup whole numbers up to at least 100, using a systematic approach and noticing patterns (e.g., 10 + _ = 70, 20 + _ = 70, 30 + _ = 70)	partition and regroup whole numbers up to at least 1,000, using a systematic approach and noticing patterns (e.g., 400 + 300 = _, 350 + _ = 500)	Investigate and represent the partitioning of numbers using appropriate materials for the year level – for example: multilink cubes, bead strings, 10s frames, and counters, at 6 months and year 1 a Slavonic abacus, ice-block sticks, and PV money, at year 2 PV money and PV blocks, at year 3. Connect students’ subitising with pattern understanding (at 6 months and year 1) and known groupings and facts (at years 2–3). Explain and discuss how to systematically record the partitioning of numbers (e.g., using partitioning diagrams, tables, vertically-listed equations).
Operations		use estimation to predict results and to check the reasonableness of calculations	use estimation to predict results and to check the reasonableness of calculations	use estimation to predict results and to check the reasonableness of calculations	Explain and spend time developing the concepts of: estimation, using the language of ‘about’, ‘more or less’, and ‘close to’ rounding, using 100s boards and number lines marked with the multiples of 10 or 100, progressing to unmarked number lines at year 3. Have students investigate and connect practical estimation situations that involve quantities and measures (e.g., the number of balls in a box, the number of steps to the door, the length of a piece of string).
			identify the nearest ten to any whole number up to 100	round whole numbers up to 1,000 to the nearest hundred or ten
	join and separate groups of up to a total of 10 objects by grouping and counting	join and separate groups of up to a total of 20 objects and find the difference between groups by grouping and counting (e.g., 9 + 6, 7 + _ = 11)	add and subtract numbers up to 100 without renaming (e.g., 53 + 21, 55 – 32)	add and subtract numbers up to at least 100 (e.g., 43 – 28, 37 + 18)	Explain and discuss addition and subtraction using representations, including: discrete materials (counters, blocks, context items), 10s frames, and number lines (at 6 months and year 1) bundles of sticks, number disks, and number lines (at year 2) PV materials (PV money, blocks, and discs) and number lines (at year 3). Connect symbols and equations with problems, using correct vocabulary (e.g., ‘add’, ‘join’, and ‘plus’ for addition). Have students practise decoding and solving word problems. At year 3, explain and connect horizontal equations and the vertical-column method for addition and subtraction. Demonstrate making estimates or mental calculations by connecting to place value, partitioning, and known facts. Use a range of problem types (e.g., result, change, start-unknown). Use worked examples and think-alouds to explain the most efficient approaches when solving problems. Have students investigate and generalise adding 0 to or subtracting 0 from a number (at year 1) and applying the commutative property of addition (e.g., 5 + 4 = 4 + 5).
		explore addition facts up to 10 and their corresponding subtraction facts (families of facts), including doubles and halves	recall addition facts up to 10, and explore addition facts up to 20 and their corresponding subtraction facts (families of facts), including doubles and halves	recall addition facts up to 20 and their corresponding subtraction facts (families of facts), including doubles and halves	Use materials to investigate addition and subtraction facts (e.g., counters, 10s frames, an abacus, multilink cubes), and use part-whole diagrams to develop subtraction facts and connect to addition facts. Explain how to record equations and families of facts, connecting with the language for each operation. Provide a range of tasks to consolidate learning and develop fluency (e.g., physical and digital games, using families of facts and, at year 3, table grids).
			identify the relationship between skip counting and multiplication facts for 2s, 5s, and 10s	recall multiplication and corresponding division facts for 2s, 3s, 5s, and 10s	Use a range of materials to represent skip counting and multiplication and division facts (e.g., 100s boards, choral counting, games, number lines, a Slavonic abacus, families of facts, and, at year 3, table grids). Provide a range of tasks to consolidate learning and develop fluency.
		multiply and divide using equal grouping or counting	multiply and divide using equal grouping or skip counting (e.g. in 2s, 5s, and 10s)	multiply a one- or two-digit number by a one-digit number, using skip counting or known facts (e.g. 4 × 6; 2 × 23)	Represent multiplication and division problems using discrete materials, pictures, diagrams, symbols, number lines, words, equations, digital tools, and, at year 3, arrays, PV materials, and bar models. Use correct mathematical language when discussing multiplication and division (e.g., multiply, groups of, sets of, rows of, equal groups, divide, share equally). Have students practise decoding and solving word problems. Connect with subitising and addition and subtraction concepts when demonstrating solving multiplication and division problems. Explain and represent division as a sharing problem (e.g., “Share 12 marbles equally among 3 friends”) or a grouping problem (e.g., “You have 12 marbles. How many groups of 3 marbles can you make?”). Use worked examples and think-alouds to explain the most efficient approaches when solving multiplication and division problems. Investigate and generalise multiplying a number by 0 or 1, dividing a number by 1, dividing a number by itself, and why we cannot divide by 0 (e.g., by trying to solve 0 × _ = 5). At year 3, explain and use the multiplicative identity (e.g., 5 × 1 = 5, 4 ÷ 1 = 4) and commutative property (e.g., 3 × 4 = 4 × 3). Demonstrate making estimates or mental calculations by connecting to place value, partitioning, and known facts.
				divide whole numbers by a one-digit divisor with no remainders, using grouping (e.g. 24 ÷ 3, 32 ÷ 4)
Rational numbers		identify and represent halves and quarters as fractions of sets and regions, using equal parts of the whole	identify, read, write (using symbols and words), and represent halves, quarters, and eighths as fractions of sets and regions, using equal parts of the whole	identify, read, write, and represent halves, thirds, quarters, fifths, sixths, and eighths as fractions of sets and regions, using equal parts of the whole and by positioning on a number line	Represent fractions using a range of materials – continuous (bar models, number lines), discrete (sets of objects), and digital. Explain and reinforce that when fractions are represented symbolically: the denominator is the bottom number and shows how many pieces a whole has been equally split into the numerator is the top number and shows how many of those parts the fraction represents. Have students practise saying, reading, and writing fractions in words and symbols. Explain how to fold paper strips to create fractions of one whole. Label the parts using words and symbols, and use them to create a fraction wall for comparing and ordering fractions. Explain that a fraction is a number that can be placed on a number line.
			directly compare two fractions involving halves, quarters, and eighths	compare and order fractions involving halves, quarters, and eighths and identify when two fractions are equivalent
		find a half or quarter of a set using equal sharing and grouping.	find a half and quarter of a set by identifying groups and patterns (rather than sharing by ones), and identify the whole set or shape when given a half or quarter	find a unit fraction of a whole number (e.g., 1—3 of 15), and identify the whole set or amount when given a unit fraction (e.g. “ 1—4 of the set is 3, what is the whole set?”)	Investigate a range of practical situations using a range of representations, including materials, drawings and diagrams, and digital tools (e.g., discrete objects, bar models, paper strips for partitioning). Make connections between: symbols, words, and pictures counting, subitising patterns and known groupings, and skip counting to solve problems (at years 1–2) skip counting and using known addition and multiplication facts to solve problems (at year 3). Use mathematical language to develop an understanding of fractions (e.g., numerator, denominator, shared equally, divide, partition, equal parts).
				add and subtract unit fractions with the same denominator (e.g. 1—8 + 1—8 + 1—8 = 3—8 )	Investigate adding and subtracting fractions within familiar contexts (e.g., cutting apples into eighths or partitioning paper strips into six equal parts, and then representing addition and subtraction with these materials). Connect representations, including symbols and equations, to drawings and materials (e.g., fraction walls, paper fraction strips), and show them on a number line.
Financial maths			recognise and order New Zealand denominations up to $20 according to their value, make groups of 'like' denominations, and calculate their value.	make amounts of money using one- and two-dollar coins and 5-, 10-, 20-, 50-, and 100-dollar notes.	Have students use play money (coins and notes) to represent practical financial situations. At year 2, compare only notes with notes or cents with cents, not a mixture of them. At year 2, investigate appropriate financial situations that involve both saving and spending. Connect to place value, addition and subtraction, and skip counting when calculating amounts.

Algebra

	During the first 6 months Informed by prior learning, teach students to:	During the first year Informed by prior learning, teach students to:	During the second year Informed by prior learning, teach students to:	During the third year Informed by prior learning, teach students to:	Teaching considerations
Equations and relationships		solve true or false number sentences and open number sentences involving addition and subtraction of one-digit numbers, using an understanding of the equal sign (e.g., 2 + 5 = 3 + _, 7 – 5 = 6 – 4 (T or F?)	solve true or false number sentences and open number sentences involving addition and subtraction of one- and two-digit numbers, using an understanding of the equal sign (e.g., 18 + _ = 17 + 6, 17 = 25 (T or F?)	solve true or false number sentences and open number sentences involving addition and subtraction, using an understanding of the equal sign	Represent the equal sign as the ‘same as’ to demonstrate it is a symbol of equivalence. Investigate number sentences using representations such as: 10s frames and discrete materials (at years 1–2) word problems with comparisons (at year 3). At years 2–3, solve number sentences that have numbers beyond what students are using in operations, so that the emphasis is on the equal relationship, not operating.
Equations and relationships	copy, continue, create, and describe a repeating pattern with two elements.	copy, continue, create, and describe a repeating pattern with three elements, and identify missing elements in a pattern	recognise and describe the unit of repeat in a repeating pattern, and use it to predict further elements using the ordinal position	recognise, continue, and create repeating and growing patterns, and describe a rule to explain a pattern	Investigate repeating and growing patterns in a range of contexts (e.g., cultural patterns, patterns in the local environment and on everyday objects). Use materials, sound, movement, and digital tools to represent and continue repeating and growing patterns. At years 2–3, demonstrate recording the pattern in a table. Form generalisations when students notice that repeating patterns constructed in different ways are similar (e.g., ‘red, blue, red, blue’ and ‘hop, jump, hop, jump’ are ABAB patterns). Help students to notice the similarities and differences between patterns by recording them. With students at year 2, generalise by using the unit of repeat and ordinal position to identify further elements in a pattern. Use mathematical language and sentence starters to support students to explain and justify how a pattern is repeating or growing and to predict further terms.
Algorithmic thinking		follow step-by-step instructions to complete a simple task.	follow and give step-by-step instructions for a simple task, identifying and correcting errors as the instructions are followed.	create and use a set of precise, step-by-step instructions for carrying out a familiar routine or task.	Represent step-by-step instructions using drawings, words, flow diagrams, and verbal instructions that form a sequence. With students, investigate sorting unfamiliar and familiar objects according to a set of instructions, directing a person or object (e.g., through an obstacle course or maze), and following and creating a set of pictorial instructions. Explain, justify, and show how a set of instructions is complete or incomplete, using think-alouds and prompts. Connect a series of events from a story, narrative, or daily timetable with statements in Number, Algebra, Measurement, and Geometry.

Measurement

	During the first 6 months Informed by prior learning, teach students to:	During the first year Informed by prior learning, teach students to:	During the second year Informed by prior learning, teach students to:	During the third year Informed by prior learning, teach students to:	Teaching considerations
Measuring			estimate and use an informal unit repeatedly to measure the length, mass (weight), volume, or capacity of an object	estimate and then reliably measure length, capacity, and mass (weight) using whole-number metric units (e.g., from tools with labelled markings)	Explain estimation, using the language of ‘about’, ‘more or less’, and ‘close to’ to help students reflect on what the quantity or measure might be. Investigate practical estimating and measuring situations, using appropriate measuring tools (e.g., at year 2, balance scales, capacity containers, informal units; at year 3, rulers, measuring jugs and cups, scales). At year 3, explain how to construct and use measurement devices, particularly rulers, measurement containers, and balance scales. Demonstrate how to accurately measure length in centimetres, mass (weight) in grams, and capacity in millilitres (at year 3).
	directly compare two objects by an attribute (e.g., length, mass (weight), capacity)	compare the length, mass (weight), volume, or capacity of objects directly or indirectly (e.g., by comparing each of them with another object, used repeatedly)	compare and order several objects using informal units of length, mass (weight), volume, or capacity	compare and order objects using metric units of length, mass (weight), or capacity	Investigate practical measuring situations to compare and order objects – for example: which is longer or shorter, is heaver or lighter, or holds more or less (at 6 months) comparing and ordering up to three objects (at year 1) explaining how identical informal units need to be used when measuring (at year 2) using tools like rulers, measurement containers, and scales (at year 3). Use mathematical language to explain and justify comparative measurement attributes (e.g., long and short; heavy, heavier, and heaviest; the same as; full and empty; more and less; wide, wider, and widest). Include descriptive te reo Māori that makes the properties of objects and shapes clear.
			turn, and describe how far an object or person has turned, using full, half, and quarter turns as benchmarks	turn, and describe how far an object or person has turned, using full, half, quarter, and three-quarter turns as benchmarks	Investigate and explain situations involving angles as ‘how far an object or person has turned.’ Have students turn physical objects and themselves. Connect turns with fractions (e.g., half, a quarter, three quarters).
	connect days of the week to familiar events and daily routines (e.g., the class timetable).	identify how the passing of time is measured in years, months, weeks, days, hours name and order the days of the week, and sequence events in a day using everyday language of time	name and order the months and seasons, and describe the duration of familiar events using months, weeks, days, and hours	identify the duration of events using years, months, weeks, days, hours, minutes, and seconds	Use visual representations to support the sequencing of events (e.g., pictorial daily timetables, calendars, day-and-month cards). Explore estimating the duration of everyday events using minutes and seconds (e.g., “How long is it until the bell rings?”). Practise recalling a sequence of events in the past and predicting future events. Use mathematical language to explain and justify comparisons of duration and points in time (e.g., before, after, soon, later, next, today, tomorrow, yesterday, 1st, 2nd, 3rd). Investigate using a calendar to work out the number of days, weeks, or months until important events (e.g., the number of days until Matariki, the number of weeks until the end of term). Explore informal ways of measuring short periods of time to identify which events last longer.
		tell the time to the hour using the language of 'o'clock'.	tell the time to the hour and half-hour, using the language of ‘past’ and 'o'clock'	tell the time to the hour, half-hour, and quarter past and quarter to the hour	Use digital and analogue clocks to have students practise telling the time. Connect using visual representations on an analogue clock to skip counting in 5s and fractions (a half and quarter). Connect the ‘structure’ of duration (minutes, hours, days) to our measures of time (“There are 30 minutes in half an hour, 60 minutes in an hour”). Identify and investigate the specific times of daily events and activities in and out of school.
Perimeter, area, and volume			visualise, estimate, and measure the perimeter and area of 2D shapes, using informal units.	visualise, estimate, and measure: the perimeter of polygons using metric units the area of 2D shapes using squares of identical size the volume of rectangular prisms (cuboids) by filling them with identical 3D blocks.	Explain and demonstrate that: perimeter is the distance around the boundary of a 2D shape area is the size of the surface of a 2D shape, or how many squares cover the surface volume is the amount of 3D space a shape takes up, or how many cubes fill the shape. Investigate familiar practical situations involving perimeter, area, and volume. Use think-alouds to demonstrate the use of visualising to identify the appropriate attribute for a measurement task and to imagine the number of units required. Explain the importance of using the same unit when measuring, and that there should be no gaps or overlaps around the outside (perimeter) and inside (area) of 2D shapes and in filled 3D shapes (volume).

Geometry

	During the first 6 months Informed by prior learning, teach students to:	During the first year Informed by prior learning, teach students to:	During the second year Informed by prior learning, teach students to:	During the third year Informed by prior learning, teach students to:	Teaching considerations
Shapes	identify, sort by one feature, and describe familiar 2D shapes	identify, describe, and sort familiar 2D and 3D shapes presented in different orientations, including triangles, circles, rectangles (including squares), cubes, cylinders, and spheres	identify, describe, and sort 2D and 3D shapes, including ovals, semicircles, polygons (e.g., hexagons, pentagons), rectangular prisms (cuboids), pyramids, hemispheres, and cones, using the attributes of shapes	visualise, identify, compare, and sort 2D and 3D shapes, using the attributes of shapes	Make available a range of 2D and 3D shapes, including tactile shapes and materials (e.g., playdough, pipe cleaners), pictures, diagrams, and digital tools. Investigate 2D and 3D shapes in the environment. Use everyday language and mathematical language (including te reo Māori) to explain and justify the describing and sorting of shapes (e.g., size, corners, colour, texture, sides, angles, faces, edges, vertices, triangle/tapatoru, square/tapawhā rite, same/ōrite, different/rerekē). Use generalisations made by students to clarify and extend understanding (e.g., “Polygons have straight sides”, “2D shapes can be identified on 3D shapes”).
Shapes				identify right angles in shapes and objects
Spatial reasoning	compose by trial and error a target shape using smaller shapes, and decompose a shape into smaller shapes	anticipate which smaller shapes might be used to compose a target shape, and then check by making the shape	anticipate which smaller shapes might be used to compose and decompose a target shape, and then check by making the shape	compose and decompose 2D shapes using the attributes of shapes (e.g., lines of symmetry), other shapes, side lengths, and angles	Make available a range of materials to compose and decompose 2D shapes (e.g., pattern blocks, attribute shapes, paper shapes, playdough, tangrams). Use think-alouds to demonstrate anticipating how small shapes can fit into or make a new shape. Use as target shapes: shapes partitioned into smaller parts (at 6 months) continuous whole shapes with no partitions (at years 1–3).
Spatial reasoning		flip, slide, and turn 2D shapes to make a pattern	recognise lines of symmetry in patterns or pictures, and create or complete symmetrical pictures or patterns	predict the result of a one-step transformation (reflection, translation, or rotation) on 2D shapes	Connect the informal vocabulary of flip, slide, and turn with the formal vocabulary of reflect, translate, and rotate. Investigate practical situations (e.g., making art, paper folding, checking symmetry with mirrors) and a range of artefacts and patterns.
Pathways	follow instructions to move to a familiar location or locate an object.	follow and give instructions to move to a familiar location or locate an object	follow and give instructions to move people or objects to a different location, using direction, distances (e.g., number of steps), and half and quarter turns	follow and create a sequence of step-by-step instructions (an algorithm) for moving people or objects to a different location	Investigate ways of moving to different locations within the classroom and in other parts of the school, using simple maps at year 3. Use picture books that emphasise positional language and movement (e.g., Scatter Cat, Bears in the Night, We’re Going on a Moa Hunt). Use spatial language and talk frames to support giving and following instructions (e.g., near, far, next to, beside, on top, under, over, down, up, left, right, turn). Make connections between: estimating distance and bodily measures (e.g., the number of steps to the door) half and quarter turns and fractions following or creating instructions and algorithmic thinking.
Pathways		use pictures, diagrams, or stories to describe the positions of objects and places.	interpret diagrams to describe the positions of objects and places in relation to other objects and places.	interpret, draw, and use simple maps to locate objects and places relative to other objects and places.

Statistics

	During the first 6 months Informed by prior learning, teach students to:	During the first year Informed by prior learning, teach students to:	During the second year Informed by prior learning, teach students to:	During the third year Informed by prior learning, teach students to:	Teaching considerations
Problem		pose a summary investigative question about a group for which the data will have categorical variables (e.g., colour, brand), and anticipate what the data might show	pose a summary investigative question about a group for which the data will have categorical variables, and anticipate what the data might show (e.g., which outcomes might be more frequent than others)	pose a summary investigative question about an everyday situation, using categorical data and discrete numerical (whole number) data, identify the variable and group of interest, and anticipate what the data might show	Show, with student input, how to: pose summary investigative questions about an area of interest identify the variable and group of interest in investigative questions.
Plan		plan to collect data by making observations or questioning others, and discuss how the data-gathering process might affect people	plan survey and data-collection questions for collecting data, identify who and what the data will measure, and discuss how the data-gathering process might affect people		Pose, with student input, survey and data-collection questions that will be used to collect the data required for the investigative question. Explain the distinction between primary and secondary data and the challenges that come with sensitive topics or questions. Investigate how survey questions and the words within survey questions can be interpreted differently by different people.
Data		collect categorical data for one variable	collect categorical data for more than one variable	collect, record, and sort data, or use secondary data sources provided by someone else	Represent data using data cards, recording sheets, and tally tables. Use data cards that represent multiple variables about an individual. Explore investigative questions using secondary data sources.
Analysis		create and make statements about data visualisations (e.g., pictures, graphs, dot plots) for the categorical data, giving the frequency for each category	create and make statements about data visualisations (e.g., pictures, graphs, dot plots) for the categorical data, comparing the frequencies of categories	create and make statements about data visualisations (e.g., pictures, graphs, dot plots, bar graphs) for the categorical and discrete numerical data	Show creating and describing data visualisations, transitioning from data cards to dot plots to bar graphs. Represent data using data cards and picture graphs (for years 1–3), frequency tables and dot plots (for years 2–3), and bar graphs (for year 3). Have students practise using ‘I notice’ statements that include the variable name and context when describing data visualisations. Explain and demonstrate ‘reading the data’ and ‘reading between the data’. Explain how to describe features of data visualisations (e.g., frequency, the least/most frequent category, modes or modal groups, highest and lowest values).
Conclusion		choose from given options the statements that best answer the investigative question		choose from given options the statements that best answer the investigative question, reflect on findings, and compare them with anticipated outcomes	Show, with student input, how to: choose the best descriptive statements that answer an investigative question collate, explain, and justify their findings to others.
Statistical literacy		agree or disagree with others’ statements about simple data visualisations (e.g., pictures, graphs, dot plots).	match statements made by others with features in simple data visualisations, and agree or disagree with the statements.	identify relevant features in others' data visualisations, connect these to descriptive statements, agree or disagree with the statements, and suggest improvements to them.	Show, with student input, how to: read and understand claims made by others and identify corresponding features in data visualisations explain agreements or disagreements with a claim made by others.

Probability

During the first 6 months
Informed by prior learning, teach students to:

During the first year
Informed by prior learning, teach students to:

During the second year
Informed by prior learning, teach students to:

During the third year
Informed by prior learning, teach students to:

Teaching considerations

Probability investigations

engage in stories or games that involve chance-based situations and:
- decide if something will happen, won’t happen, or might happen
- identify possible and impossible outcomes (e.g., for what might happen next).

engage in chance-based investigations about games and everyday situations to:
- anticipate and then identify possible outcomes
- collect and record data
- create data visualisations for frequencies of possible outcomes (e.g., lists, pictures, graphs)
- describe what these visualisations show
- answer the investigative question
- notice variations in outcomes (e.g., how often each of the numbers on a dice come up)

Investigate probability by playing games of chance using physical objects (e.g., dice, coins, spinners, pulling things out of a hat).

Explain and show how to:

list possible outcomes
visualise frequencies of outcomes
use the vocabulary that indicates the relative order of probabilities from impossible to certain (i.e., impossible, unlikely, possible, likely, certain).

Critical thinking in probability

agree or disagree with the statements made by others about chance-based situations.

explain and question statements about chance-based situations, with reference to data.

Show, with student input, how to:

read and understand claims made by others about chance situations
match statements with the relevant chance situation being described
explain and justify why they believe a statement is true or not.

The language of mathematics and statistics: Phase 1

	At 6 months Students will know the following words:	Year 1 Students will know the following words:	Year 2 Students will know the following words:	Year 3 Students will know the following words:
Number	add, plus, join altogether biggest, smallest combine, separate count group how many in between more, less next, before, after ordinal (1^st, 2^nd, 3^rd etc.) take away, minus	count on, count back digit double, halve equal group equal part fair share forwards, backwards fraction half, quarter odd, even partition set share skip count subtract sum, difference whole set	cent, coin, dollar, note denominator eighth estimate, estimation money multiply, divide numerator place value quantity, amount regroup	operation round third, fifth, sixth unit fraction
Algebra	continue copy next pattern repeat	changed, unchanged element equal, equivalent equation number sentence repeating pattern true, false unit of repeat zero	error predict	complete, incomplete growing pattern rule sequence term
Measurement	comparative words (long, taller, heaviest etc.) full, empty heavy, light height length measure, weigh same as short, tall, wide, large, small, big	capacity day, week, month, year days of the week distance earlier, later hour morning, afternoon, evening o’clock starting point, end point weight	area full turn, half turn, quarter turn half past months of the year perimeter seasons of the year surface width	gram litre, millilitre measuring jug or cup metre, centimetre metric minute, second quarter past, quarter to ruler three-quarter turn unit volume weighing scale, balance scale
Geometry	flip positional language (next to, above, below, under, up, down, on top of, inside etc.) side, corner size (big, small, long, short) square, triangle, circle straight, curved, round turn	2D shape 3D or solid shape cube, cylinder, sphere edge, face slide rectangle	direction left, right oval, semicircle, polygon (hexagon, pentagon), rectangular prism (cuboid), pyramid, hemisphere, cone position symmetry, line of symmetry vertex	location quadrilateral reflect, reflection right angle rotate, rotation transform, transformation translate, translation
Statistics		data dot plot information most, least picture graph survey tally	category graph notice outcome statement table title	bar graph claim finding frequency variable
Probability		chance possible, impossible will happen, won’t happen, might happen	agree, disagree anticipate certain, uncertain likely, unlikely list	probability

Mathematics and Statistics Learning Area Years 0–8 glossary

Abstract	Symbolic representation of a concept.
Acceleration	Acceleration or accelerated learning is where students are enabled to learn concepts and procedures more rapidly than the expected rate of progress. Accelerated learning approaches involve teaching students year-level content and experiences and supporting them with appropriate scaffolds to make this work accessible.
Additive identity	Zero will not change the value when added to a number. For example, 16 + 0 = 16.
Algorithm	A set of step-by-step instructions to complete a task or solve a problem.
Algorithmic thinking	Defining a sequence of clear steps to solve a problem.
Argument	Providing an idea or finding that is based on reasoning and evidence.
Associative property	A property of operations when three numbers can be calculated (addition or multiplication) in any order without changing the result. For example, (4 + 3) + 7 = 4 + (3 + 7) because 7 + 7 = 4 + 10, and (4 x 3) x 5 = 4 x (3 x 5).
Assumptions	A proposition (a statement or assertion) which is taken as being true with respect to a given context.
Attribute	A characteristic or feature of an object or common feature of a group of objects —such as size, shape, colour, number of sides.
Base 10	Our number value system with ten digit symbols (0-9); the place value of a digit in a number depends on its position; as we move to the left, each column is worth ten times more, with zero used as a placeholder; to the right, the system continues past the ones’ column, to create decimals (tenths, hundredths, thousandths); the decimal point marks the column immediately to the right as the tenths column.
Benchmarks	A reference point that we can use for comparison or estimation. For example, “My finger is about one centimetre wide.”
Categorical variables	A variable that classifies objects or individuals into groups or categories. For example, hair colour, breed of dog.
Chance	The likelihood that an outcome will occur.
Claim	A statement of what the student believes to be correct.
Commutative property	In addition and multiplication, each number can be operated in any order. For example, 5 + 6 = 6 + 5.
Compose and decompose	Compose is to make a shape using other shapes. Decompose is to break a shape into other shapes.
Comparison investigative question	An investigative question that compares a variable across two clearly identified populations or groups. For example, “I wonder if girls in our class tend to be taller than boys in our class?”
Conceptual understanding	The comprehension of mathematical concepts, operations, and relations by connecting related ideas, representing concepts in different ways, identifying commonalities and differences between aspects of content, communicating their mathematical thinking, and interpreting mathematical information.
Conjecture	A statement whose truth or otherwise is not yet determined but is open to further investigation.
Constant	A constant term is a fixed value that will not change.
Continuous materials	Models based on relative length or area, such as a number line, fraction wall, bar model.
Data	A collection of facts, numbers, or information; the individual values of which are often the results of an experiment or observations.
Data ethics	The principles behind how data is gathered, protected, and used; at the core of ethical practice is the need to do good and to do no harm.
Data visualisations	A graphical, tabular, or pictorial representation of information or data.
Deduction	Make a conclusion based on knowledge, definitions, and rules.
Digital tools	Digital applications, calculators.
Discrete materials	Separate objects that can be counted and grouped. For example, counters, ice block sticks.
Discrete numerical variables	Variables that can be counted and have a limited range of possibilities. For example, number of students in each team, the result of rolling a die.
Disinformation	False information spread deliberately to deceive others.
Distribution	In mathematics, distribution describes spreading terms out equally across an expression; in statistics, distribution describes how data values are spread across the range of values collected.
Distributive property	An operation is said to be distributive over another operation if it can take priority over the operation used for combination within brackets. For example, 6 × 17 = 6 × (10 + 7) = (6 × 10) + (6 × 7) = 60 + 42 = 102.
Efficient	A procedure is said to be efficient when it is carried out in the most simple and effective way.
Element in a pattern	In a repeating pattern, an element is the repeating core. In a growing pattern, an element is a section of the pattern. For example, in the Fibonacci sequence 1, 1, 2, 3, 5, 8, the next element is the sum of the previous two elements (5 + 8 = 13).
Equation	A number statement that contains an equal sign. The expressions on either side of the equal sign have the same value (are equal).
Equivalent fraction	Two different fractions that represent the same number are referred to as equivalent fractions. For example, 1—2, 2—4, 3—6, and 4—8 are equivalent fractions because they represent the same number.
Estimate	A rough judgement of quantity, value, or number. In statistics, an assessment of the value of an existing, but unknown, quantity. In probability, the probability of an outcome in an experiment.
Event	One or more outcomes from a probability activity, situation, or experiment.
Evidence	Information, findings, data that support (prove) a statement or argument.
Expression	Two or more numbers, operations or variables connected by operations. Expressions do not include an equal or inequality sign.
Families of facts	A group of equations that use the same numbers. For example, 3 x 2 = 6, 2 x 3 = 6, 6 ÷3 = 2, 6 ÷ 2 = 3.
Generalisation	To recognise and describe patterns in relationships.
Growing pattern	A pattern where there is a constant increase or decrease between each term. For example, 5, 10, 15, 20.
Horizontal method	Representing the operation as an equation across the page, often partitioning one of the numbers into tens and units. For example, 16 + 23 = 16 + 20 + 3.
Inequality	A statement in which one number or expression is greater or less than another.
Inference	Making a conclusion based on evidence and reasoning.
Informal unit	A non-standard unit used to measure. For example, blocks, pens, fingers. The informal units used should all be the same size.
Interpret	To make meaning from something.
Inverse operations	The opposite operation, so addition is inverse to subtraction, and multiplication is inverse to division. They are useful to check calculations. For example, to check 4 x 5 = 20, we can see if 20 ÷5 = 4.
Limitations	Possible missing evidence or information.
Mathematical modelling	An investigation of the relationships and behaviours of quantities in physical, economic, social, and everyday contexts; used to analyse applied situations and make informed decisions, starting the model with forming assumptions.
Misconception	A misunderstanding about a procedure, method or definition in mathematics or statistics. This could be about which procedure is needed, how the procedure or method should be followed or an incorrect definition. For example, thinking that 2.5 is the decimal form of 2/5.
Misinformation	Incorrect information (mistakes).
Multiplicative identity	When a number is multiplied by 1, it does not change its value. For example, 15 x 1 = 15.
Number sentence	An equation or inequality expressed using numbers and mathematical symbols. For example, 10 = 3 + 7 + 5 + 5.
One step transformation	One change in a shape's position or size. For example, a triangle is flipped (reflected).
Ordinal	The numerical position of the element in the sequence. For example, first, second, third.
Orientation	The angle that an object is positioned.
Outcomes	A possible result of a trial of a probability activity or a situation involving an element of chance; could also refer to a result or a finding.
Partition and regroup	Partitioning is the process of "breaking up" numbers. For example, 55 = 50 + 5. Regroup means to rearrange the formation of the group. For example, 55 = 40 + 15 or 55 = 30 + 25.
Primary data	Data collected first-hand for a specific purpose. For example, a survey, experiment, or interview.
Probabilistic thinking	Considering the likelihood (chance) of an outcome occurring; this is based on logic and reasoning.
Probability experiment	A test that can be carried out multiple times in the same way (trials). The outcome of each trial is recorded.
Procedural fluency	Choosing procedures appropriately and carrying them out flexibly, accurately, and efficiently. It is not the same as memorisation of facts and steps; rather it is being able to activate what you know and when to use it.
Procedure	A sequence of operations carried out in a specific order, such as the procedure to multiply two numbers, or the procedure to measure an object.
Quantifying	Expressing a quantity using numbers.
Rational number	All integers, fractions, and decimals.
Reasoning	Analysing a situation and thinking and working mathematically to arrive at a finding. Inductive reasoning is where an explanation is made based on observations and data. For example, “18 out of 22 people in our class like grapes, so grapes are the favourite fruit of our class.” Deductive reasoning is where we apply a known rule or fact to solve a problem. For example, prime numbers have two factors (itself and one), 4 has three factors, so it is not a prime number.
Relational	Symbols that show relationships between elements (terms) in an expression. For example, =, <, >
Repeating pattern	A pattern containing a 'unit of repeat'. For example, red, green, blue, red, green, blue.
Secondary data	Data collected by someone else, or a process, and/or obtained from another source. For example, online, books, other researchers.
Subitise	Instantly recognise the number of items in an arrangement without counting.
Summary investigative question	A question that asks about the overall distribution of the data or what is typical and reflects the population or group. For example, “I wonder how many pets are in our class? I wonder what the heights of the students in the class are?”
Tangible and intangible	Tangible is an object that can be touched. For example, a group of blocks. Intangible is a quality or measurement that cannot be touched. For example, colour or length.
Term in a pattern	One of the numbers in a pattern or sequence. For example, for 2, 4, 6, 8, the second term is 4.
Theoretical probability	A calculation of how likely an event is to occur in a situation involving chance.
Uncertainty	In probability, when the chance of an event occurring is unknown.
Unit of repeat	The part of a repeating pattern that repeats. The part is made up of several elements
Variables (statistics and algebra)	A property that may have different values for different individuals (statistics) or that may have different values at different times (statistics and algebra).
Variation	The differences seen in the values of a property for different individuals or at different times.
Vertical column method	The method for solving an operation by recording numbers in columns according to place value, working down the page.
Visualisation	To mentally represent and manipulate.

NZC - Mathematics and statistics (Phase 1)

Tags

Page quick links

About this resource

Progress outcome by the end of year 3 (Foundation)

Teaching sequence – Phase 1 (Years 0-3)

Explicit teaching

Positive relationships with mathematics and statistics

Rich tasks

Communication in mathematics and statistics

Number

Algebra

Measurement

Geometry

Statistics

Probability

The language of mathematics and statistics: Phase 1