Place value of whole numbers to 3 places
This resource supports teachers to assess and find appropriate activities for students who need acceleration in their understanding and application of place value of whole numbers to 3 places.
About this resource
New Zealand Curriculum: Level 2
Learning Progression Frameworks: Additive thinking, Signpost 5 to Signpost 6
These activities are intended for students who are yet to understand place value with two- and three-digit numbers. By the end of level 2 of The 2007 New Zealand Curriculum, and step 5 of Learning Progression Frameworks, students are expected to know most, or all, of their addition and subtraction basic facts (number bonds to 20). Some students will still need to work on their basic facts as they learn about place value with two-digit and three-digit whole numbers.
Place value of whole numbers to 3 places
The following diagnostic questions indicate students’ understanding of whole number place value to 3 digits. The questions are given in order of complexity. If the student answers a question confidently and with understanding, proceed to the next question. If not, use the supporting activities to build or strengthen fluency and understanding. Allow access to pencils, paper, and a calculator when suggested in the notes.
The questions should be presented orally and in written form (Place value of whole numbers to 3 places questions) so that the student can refer to them. The questions may be changed to other contexts that are engaging to your students.
Required materials
See Materials that come with this resource to download:
- Place value of whole numbers to 3 places questions (.pdf)
[Prepare a collection of 47 objects, such as ice block sticks, buttons, or interlocking cubes.]
Here are 47 ice block sticks. [Record 47]
I want you to put them into bunches of ten.
- How many bunches will you make?
- Will you have any left over? How many?
Signs of fluency and understanding
Anticipates that 4 collections of ten are possible with 7 objects remaining. Avoid asking the student to group the objects physically.
What to notice if they don’t solve the problem fluently
Based on visual appearance, the student speculates about how many collections of ten can be made and how many ones will remain. This indicates that the student needs opportunities to connect two-digit numbers with groups of ten and remaining ones.
Supporting activity
Please read this number [Write 29].
- What is the number that is one more than 29?
- What is the number that is ten more than 29?
- What is the number that is ten less than 29?
Signs of fluency and understanding
Reads 29 correctly and knows that one more than 29 is 30. Finds ten more by adding one to the tens digit (to get 39) and ten less by subtracting one from the tens digit (to get 19).
What to notice if they don’t solve the problem fluently
Counting up by ones, possibly by beginning from a trusted number, such as 25, 26, 27, 28, 29, 30, to find one more than 29. This may indicate that the student needs opportunities to count up and back by ones through the decades.
Counting up or down, by ones to find the number that is ten more or ten less. This is likely to occur with finger tracking to monitor the count. This may indicate that the student needs opportunities to count in tens forwards and backwards from any number and to associate the counting with changes in quantities.
Supporting activity
Here are some ice block sticks. (Other place value-based materials like BeaNZ in canisters, play money, or place value blocks are also suitable).
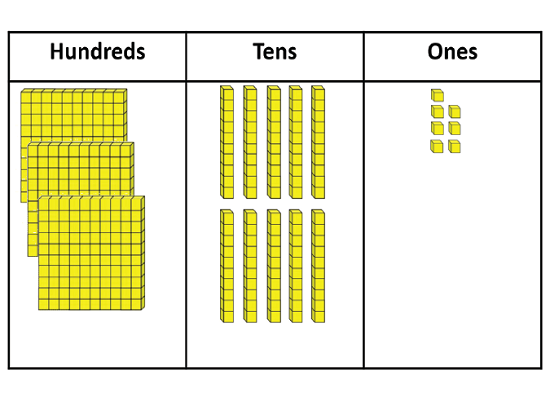
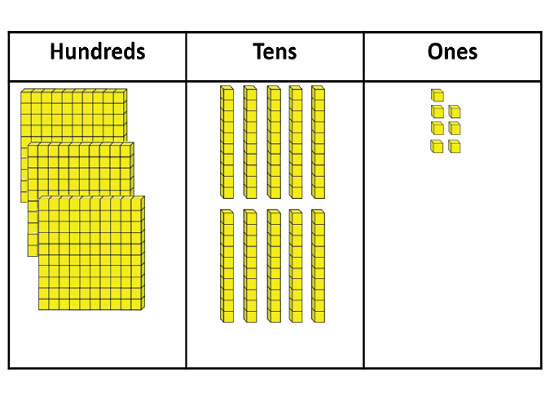
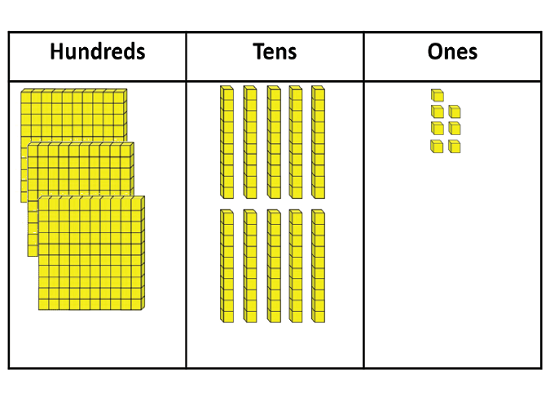
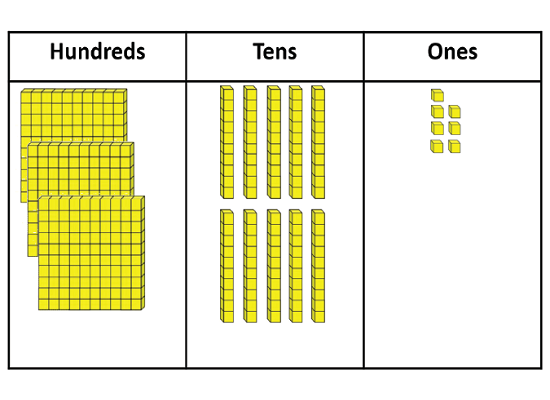
Please make this number of ice block sticks. [Write 458]
Signs of fluency and understanding
Creates the correct amount by counting 4 hundreds, 5 tens, and 8 ones. This indicates that the student connects the digits in each place with quantities.
What to notice if they don’t solve the problem fluently
Confuses the places and chooses the wrong number of each unit or treat all places as the same unit. This indicates that the student needs opportunities to connect the numerals in 3-digit numbers with place value-based materials.
Ignored the meaning of the digits and counts in ones. Stop the student if this occurs.
Supporting activity
Please read this number [Write 567].
Start at 567 and count forwards in tens. (Let the student continue until they reach 627.)
Start at 567 and count backwards in tens. (Let the student continue until they reach 487.)
Signs of fluency and understanding
Reads 596 correctly. Counts up through 600 and back through 500, fluently adjusting the appropriate digits, i.e., 587, 597, 607 and 517, 507, 497. This indicates that the student is able to control counting sequences of three-digit numbers by tens.
What to notice if they don’t solve the problem fluently
Does not count up and back through a century in tens. This indicates that the student needs opportunities to connect counting sequences with place value-based quantities. In particular they would benefit from practice at collecting ten tens to make 100, and decomposing 100 to make ten tens.
Supporting activity
You get $382 from the bank. [Record the amount.]
They pay you in $10 notes.
- How many notes do you get? What coins do you get?
Signs of fluency and understanding
Knows that 382 is 380 + 2. Understands nested place value by showing that 380 contains 38 tens. The student may say they will get a $2 coin as well.
What to notice if they don’t solve the problem fluently
Knows that ten tens are in 100. Counts 10, 20, 30 tens to reach 300, then counts in units of ten, 310, 320, 330, 340, …, 380 to get an answer of 38 tens. This indicates that the student needs experience anticipating the number of tens in three-digit numbers.
Counts up in tens to reach 380, tracking tens as they go. Usually the student will use some recording, such as tally marks, to organise the counting of tens. This indicates that the student needs experience composing hundreds from tens and decomposing hundreds to form ten tens.
Supporting activity
Teaching activities
One and ten more or less with two-digit whole numbers
The purpose of this activity is to support students in counting fluently forwards and backwards in units of one or ten. They should be able to start with any two-digit number and connect counting in tens or ones with changes in the quantity.
1 of 5Connecting two-digit place value with grouping
The purpose of this activity is to support students in understanding that tens and ones digits represent units of different sizes, and that therefore represent quantities in a two-digit whole number.
2 of 5Connecting three-digit place value with grouping
The purpose of this activity is to support students in understanding the quantities that three-digit whole numbers represent. Students come to know that the hundreds, tens, and ones digits represent units of different sizes.
3 of 5Finding the number of tens in three-digit numbers
The purpose of this activity is to support students in understanding that tens are nested in hundreds, and ones are nested in both tens and hundreds. They also develop fluency in renaming three-digit numbers in multiple ways.
4 of 5Counting sequences with three-digit numbers
The purpose of this activity is to support students in counting fluently forwards and backwards in units of one, ten, and one hundred. They should be able to start with any three-digit number and connect counting in hundreds, tens or ones with changes in the quantity.
5 of 5
The quality of the images on this page may vary depending on the device you are using.