Measuring beads
In this unit, we compare the weight of students favourite soft toys directly and then indirectly using beads. Although the technically correct term to use is mass, the term weight is used here.

About this resource
Specific learning outcomes:
- Compare a group of three or more objects by mass.
- Measure mass using non-standard units.
Measuring beads
Achievement objectives
GM1-1: Order and compare objects or events by length, area, volume and capacity, weight (mass), turn (angle), temperature, and time by direct comparison and/or counting whole numbers of units.
Supplementary achievement objectives
NA1-1: Use a range of counting, grouping, and equal-sharing strategies with whole numbers and fractions.
NA1-3: Know groupings with five, within ten, and with ten.
Description of mathematics
In this unit, the students use balance scales and beads to measure the mass of different objects. Although the technically correct term to use is mass rather than weight, we believe that at Level 1, it is confusing to be "particular" about the difference. As the students will be most familiar with the term weight, we believe it is reasonable to use it to describe these activities.
Measuring the mass of objects using non-standard or informal units is the third stage in the learning sequence of measurement. Initially measuring with non-standard, but familiar, units allows the students to focus on the process of repeatedly using a unit as a measuring device. Students should be given lots of opportunities to use balance scales or "home-made" beam balances and objects such as blocks, marbles, and beads to measure and compare the mass of a wide range of objects.
From the earliest of these experiences, students should be encouraged to estimate. Initially, these estimates may be nothing more than guesses, but estimating involves the students developing a sense of the size of the unit. As everyday life involves estimates at least as frequently as exact measures, the skill of estimating is important.
At this stage, students can also be introduced to the appropriateness of measuring units. For example, a block is more appropriate than a paper clip for measuring the mass of a book.
Although non-standard units reinforce most of the basic measuring principles, students need to realise that they are limited as a means of communication. This can be highlighted through activities that involve the students measuring a single object using non-standard units, for example, books.
Beads are an example of a non-standard measuring unit. They reinforce most of the principles that underpin measurement and allow students to find out that:
- You must not change the unit being used when you are measuring an object.
- Units are chosen for their convenience and appropriateness for the object being measured.
Links to numeracy
This unit provides an opportunity to develop number knowledge in the area of Number Sequence and Order, in particular the development of the forward number word sequence. It can also be used to develop the strategy of counting to solve comparison problems.
To develop students’ knowledge of the forward number word sequence, draw students' attention to the number sequence used to count the number of beads needed to measure the length or mass of each teddy.
You should also ask questions such as:
- How many beads will you need to measure around Teddy’s tummy?
- Let’s count together to see if you’re right.
- It measured 28 rods; what number is one more than 28? What number is one less than 28?
To develop the strategy of counting on to solve comparison problems, ask students to compare the differences in mass (where the difference is not too large). Encourage students to start counting at the lowest measurement and count-on to see how much longer the second measurement is. If needed, the two bags of beads can be lined up next to each other to make it clear which objects should be included in the count. Use comparative statements to develop this further:
- Tane’s teddy is the same weight as 7 beads.
- Sarah’s teddy is the same weight as 10 beads. It is 3 beads heavier than Tane’s.
- Students can keep track of the count using their fingers.
- Steven’s teddy is the same weight as 36 beads, and Jason’s teddy is the same weight as 40 beads. How much heavier is Steven’s teddy than Jason’s? “… 37, 38, 39, 40 ... that's 4 more beads".
- Lucy’s rabbit is the same weight as 15 beads, and Jane’s bear is the same weight as 18 beads. What is the difference between these two weights? “… 16, 17, 18 … that’s 3 more beads."
Opportunities for adaptation and differentiation
The learning opportunities in this unit can be differentiated by providing or removing support for students and by varying the task requirements. Ways to differentiate include:
- carefully choosing which toys are being compared in each instance. It is easier to differentiate between toys that vary more in size
- choose a size of beads that provides an appropriate level of challenge. Smaller beads will measure more accurately but require more precision
- providing opportunities for students to work in pairs and small groups in order to encourage peer learning, scaffolding, extension, and the sharing and questioning of ideas
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities
- for Mystery Toys, choose whether to include toys that are quite similar; this will make the task more challenging.
This unit is based on making measurements of students' own toys, which should be engaging to them. The activities can be adapted to other contexts; for example, you may prefer to use the class toys or ask students to bring a toy. You might explore the mass of different objects that are relevant to students' cultures or to learning from other curriculum areas (for example, the mass of poi, ngā rakau, and different sports equipment).
Te reo Māori kupu such as ine (measure), tatau (count), taumaha (heavy, weight), taimāmā (light, not heavy), and ine-taumaha (scale for measuring weight) could be introduced in this unit and used throughout other mathematical learning. You could also encourage students who speak a language other than English at home to share the words related to mass, weight, and measurement that they use at home.
Required materials
- beads
- bead measuring strings
- small grip-lock plastic bags
- balance scales
- soft toys (or other items) brought from home
- blank cards
Activity
1.
We begin the week by looking at two soft toys of similar size but of different masses. Distribute toys to students or ask them to pick one. Ask a student to put their toy in the centre of the circle.
- Which of these toys do you think is the heaviest? Why do you think that?
- How could you check?
You might extend this activity to objects not in the classroom, e.g., what do you think is heavier—a gecko or a kiwi?
2.
Let the students take turns comparing the mass of the toys by holding them.
- How could you describe the weight of the two toys?
List these on the board.
3.
Introduce another soft toy.
- Is this toy heavier, lighter, or in-between?
Put the three toys in order of weight.
4.
Place a balance scale in the centre of the students.
- Do you know what this is?
- What can you tell me about scales?
- How could we use these to check the order of our toys?
Have the students share their ideas and use the balance scales to check the order of the toys.
5.
Place one of the toys (the lightest) on one end of the balance scales.
- How many of these beads do you think it would take to balance the toy?
Ask for estimates.
6.
Give each student a bag of 10 beads. Ask them to check the beads in their bag. Add the bags to the balance scale until the toy is balanced. This may require using some individual beads at the end.
7.
Count the number of beads together: 10, 20, 30, 31, 32, 33.
8.
Look at the second toy.
- How many beads do you think this toy weighs?
9.
Take turns adding bags of beads to the scales, counting as they are added. Record, for example:
- Rabbit: 33 beads
- Bear: 45 beads
10.
If you have sufficient balance scales, let the students work in small groups to weigh other toys or classroom objects. Alternatively, leave the balance scales set up on the math table for the students to take turns using.
Over the next three days, we measure our toys and record them on "mystery" cards. As well as weighing our toys, we measure their heights and around their tummies using bead measuring strings. We then try to match the mystery cards to the toys. You could adapt this session to focus on measuring other items related to a more meaningful context, such as different pieces of sports equipment or different items from a range of cultures.
1.
Demonstrate how to take and record the three measurements.
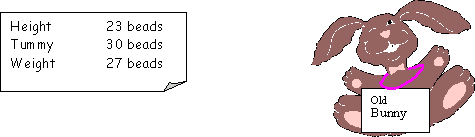
2.
Have the students take the measurements of their own toys. As the students work, assign each student a number to go on their "mystery" card. Enter this number next to the student’s name and the toy’s name on a class list.
3.
After the students have measured their toy, collect the "mystery" cards. Get each student to put a name necklace on their toy.
4.
Arrange the toys in various places around the room.
5.
Now play "Mystery" Toys. Get pairs to select, at random, a mystery card from the pile.
- Students estimate which toys it might be and then measure to find a match.
- When the pairs are sure they have found the right toy, they tell the toy's name and code number to the teacher, who checks against the class list.
- If they are correct, they get another card to solve. If not, they continue measuring.
6.
At the end of each session, gather the students together to discuss the day’s work.
- How did you go about finding your mystery toy?
- Which measurement on the card was the most useful?
Today we tried to find the mystery toy without doing any measuring.
1.
Discuss with the class the strategies that they used while finding the mystery toys.
- What did you do to work out the mystery toys?
2.
Show the class another mystery card and tell them that today they are going to try to work out the toy without doing any measuring.
3.
Give each student a copy of the information or write it on the board.
4.
Give the students time to walk around looking at the toys to see if they can figure out which one is the mystery one. Encourage students to do their own thinking and make their own decisions. When they have each made a decision, ask them (or help them) to write down their reasons for selecting the toy.
- Write down the name of the toy that you think it is.
- Write down all the reasons you used to think it was the mystery toy. You can use pictures and words.
5.
Share decisions and reasons. Focus on the reasoning rather than whether the students actually guessed the toy or not.
Home link
Dear parents and whānau,
This week at school, we have been using beads to weigh our toys. Ask your child to tell you about the Mystery Toy game we have been playing.
At home this week, your child is to try to find something that they think would weigh 15 beads. They can bring these objects to school to check out the balance scales. If they don’t guess correctly on their first attempt, they can keep trying until they find something that weighs 15 beads.
The quality of the images on this page may vary depending on the device you are using.


