The activities are mostly open-ended, meaning they cater to a range of achievement levels. It is expected that students have some experience naming and classifying basic geometric shapes, measuring lengths in centimetres and metres, and translating, reflecting, and rotating shapes.

In this session, students apply their geometry knowledge to solve two puzzles about the stars in the Matariki cluster. They will find out how the brightness of each star was used to predict the coming year, such as when to plant crops, and apply probability to estimate the chances of a ‘perfect year’.

1.

Begin by showing the students a picture of the Matariki cluster. These can be easily found by doing an online image search. Most pictures have the seven stars, though, as the students will find out, there is now a conjecture that nine stars were used to forecast the New Year. Tell the students that two stars, Pōhutukawa and Hiwaiterangi, are now treated as part of the Matariki cluster. Previously, it was believed that only seven stars were visible to the naked eye

2.

Ask: 

• Why is Matariki a special time in Aotearoa (New Zealand)?

The first new moon after the rising of Matariki in June signals the middle of winter and the beginning of a new year. It is a time to celebrate life and remember those who died in the previous year.

3.

Put the students into groups of three. Each trio will need a set of six puzzle cards (two each) and a diagram of the Matariki star cluster (see Matariki L3-1). Tell the students that they need to use the clues on the cards to name each star. They will need to work together, as each clue is important. You may need to clarify words like arc and trapezium. You could also provide a reference chart of shapes and shape names for students to refer to. Encourage students to find definitions online rather than tell them. After a suitable period of time, bring the class back together to name each star.

4.

Use Matariki level 3-1 to reveal the star names, working through the set of clues systematically. Tell the students that the stars of Matariki were used to forecast the coming years and make decisions about planting and food gathering. Although the time of forecasting varied from iwi to iwi it was always around the middle of winter. 

5.

Put them back into their trios to solve the second co-operative puzzle, Matariki L3-2. There are five cards. If they use the clues correctly, they will find out which aspect of life each star was assigned to. Discuss which clues students used to determine each star’s responsibility. Use Matariki level 3-2 to check their answers. The PowerPoint shows how a matrix can be used to organise the information.

6.

You may like to show your students this video of the seven sisters. The sisters behave like ‘wandering stars’ so they are given jobs to do.

7.

Tell the students that one role of a Tohunga (expert) is to read the Matariki stars at dawn of the new moon. If the star cluster is bright, clear, and appears ‘spread’ this forecasts good news for the year ahead. If the star cluster is dull, fuzzy, and appears ‘close together’ this indicates a year that will be lean. In some iwi, individual stars are read, so the long range forecast is more specific. In particular, the stars related to food gathering or growing are looked at closely. Find out about the beliefs of your local iwi, and integrate these into the lesson. 

8.

Explain that environmental conditions, like weather, are hard to predict, especially in the long-term. Therefore, these conditions are like a game of chance. There are six stars related to food. Highlight those stars (see slide three). Ask your students to highlight the stars on their copy of Matariki L3 2 and put in the direction arrows. Next, simulate the chances of the star being bright or fuzzy. Use a standard dice, labelled 1-6. If the dice number is even, then the star is bright, so highlight it with a felt pen or highlighter. If the dice number is odd, colour the star grey as fuzzy and hard to see. Work your way around all eight role stars in the direction of the arrows. Look at the completed cluster. 

9.

Ask: 

• What would the Tohunga predict this year? 

Students might say that the year will be windy and sea fishing will be poor. However, fishing for freshwater food, like eels, will be plentiful. The crops will do well, and the rain will be balanced, not too much and not too little. The forest will have a lean year, so don’t count on lots of birds to eat. 

10.

Tell the students to simulate the brightness of the stars using dice and write a prediction for the year ahead. Gather the class together and share some star pictures and predictions. Students should notice the variation in the pictures. Are any patterns the same?

11.

Ask: 

• How many bright stars and how many dull stars did you expect to get? Why?

Do students notice that there is a one half (50%) chance of getting each option on a dice roll?

12.

• How likely is it that every star will be bright?

This is very unlikely. With only two stars, the chances are one in four. With three stars, the chances are one in eight. The tree diagram and pattern of probability can be extended if your students understand them. You might take this chance as an opportunity for students to construct their own tree diagrams relevant to the chance of experiencing windy conditions or catching different types of freshwater food.

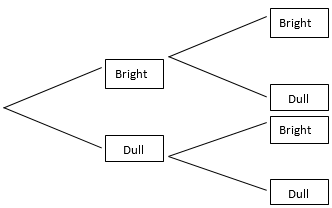
13.

The chance of all eight stars being bright is one in 256 (1/256). However, it is possible that a picture looks like that or the matching alternative of all six stars being grey. The outcomes are unlikely but not impossible.

In this session, the students look for patterns in tukutuku patterns. In particular, they find ways to count the number of tuinga (cross stitches) in a given pattern and use their counting strategy for one member of the pattern to predict further members. They are also encouraged to look for relationships between variables in each tukutuku pattern.
The session is driven by two resources:

• Matariki level 3-3 provides coloured slides of each pattern to support students to structure (organise) the pattern
• Matariki L3-3 provides students with a template to record what they see without spending time laboriously copying the patterns

1.

Give each student a copy of Matariki L3-3 to record their thinking and follow this sequence:

2.

Slide one: Discuss how tukutuku panels are created by cross-stitching horizontal and vertical rods or wooden panels with square arrays of holes. The rods are called kaho and the stitches are called tuinga.

3.

Slide two: Ask the students to describe how the pattern grows. They should notice the shape is triangular (tapatoru means triangle) and that each layer requires more stitches than the one before. Some students might predict how many stitches will be needed for the next layer. There will need to be twelve stitches on each side of the triangle, so 33 stitches in total, allowing for the overlaps at the corners.

4.

Slide three: Ask your students to find a way to count the number of stitches in ‘chunks’ rather than one at a time. Get them to share how they saw the pattern with a partner before you have a class discussion. If you have an interactive whiteboard, you might draw on the patterns to highlight the ‘chunks’ students are using or have students do so themselves.

5.

Slide four: Finding out if the strategy you applied to one member of the pattern works on further members is an important step in generalisation. Get students to share their strategies with a partner before discussing possibilities with the class. Encourage your students to find manageable ‘chunks’ that will be in any triangular layer pattern like that. For example, students might count the bottom side, then what remains of the right side, and finally the inclined side. This produces an interesting sum of 9 + 8 + 7 = 24 crosses.

• But 24 equals 3 x 8. Is that important? What would the sum for the next pattern be?

6.

Slides five to seven provide examples of how students might structure the six crosses across a layer. It is also important to consider how each hypothetical student would record what they see.

7.

Slide five: Kiri counts the crosses on one side and knows that the other two sides have the same number of crosses. She also knows that if she calculates 3 x 6 = 18 that will be three crosses too many because the corners are double counted. So she would record 3 x 6 – 3 = 15.

• That’s interesting because 3 x 6 – 3 = 3 x 5 again!

8.

Slide six: Sione tries to avoid double counting the corners. He realises that if he includes only one corner on each side, then he counts all the stitches. There are six stitches on each side, less one corner, gives five stitches. So he writes 3 x 5 = 15.

9.

Slide seven: Taylor counts the middle crosses on each side, leaving the corner stitches out. That gives her three sides, with four on each side. 3 x 4 = 12 but she also needs to add on the three corner stitches to get 15.

• But 3 x 4 + 3 = 3 x 5 again!"

10.

Slide eight: Ask students to attempt this task independently and record on the copymaster how they worked it out. The problem is to imagine a tapatoru (triangle) layer being added ‘a long way further on’ in the pattern. This requires a different type of structuring. Students need to apply ‘chunks’ they saw in the examples to create a feasible further member of the pattern. Some may not have observed that the number of crosses on each side is always a multiple of three. Once a bottom side is created, the other sides need to have the same number of crosses.

11.

Look for students to apply the strategies used by themselves and others to count the stitches in their ‘further on’ layer. Encourage them not to draw every stitch and to imagine what must be there. Students might just record equations like 99 + 98 + 97 = 294 (for a tapatoru layer with 99 stitches along the base side) or 3 x 300 – 3 = 997 (for a tapatoru layer with 300 stitches on each side).

12.

After a suitable period of investigation, ask the students to share their answers in small groups so you can observe the discussion. You might choose to highlight solutions you think are particularly insightful and get the student responsible to share their strategies, particularly for counting the stitches.

13.

Slides nine to eleven: Follow a similar process with the pātiki (flounder) design, except expect the ways to structure the pattern to come from your students. Ask them to record how they found the total number of stitches (slide 10) using an equation and link that calculation to ‘chunks’ of the layer. Slide 11 gives them a chance to imagine how an example of the pattern might look ‘further on’.

14.

Some students might notice that although the pattern looks different, it is actually quite similar to the tapatoru pattern, and similar thinking can be used. The diamond layers (not a mathematical word) are actually squares that could be rotated so the sides lie vertically and horizontally. Viewed like that, the same strategies used to count stitches on three sides can be applied to four sides.

15.

The length of the sides (in crosses) is always a multiple of four, except for the first stitch in the middle. So the pattern of crosses that are added goes like this:

16.

Students at Level Three are not expected to write algebraic formulae, though some may represent a rule in words or invented symbols, e.g., "If you count the number of crosses along one side of the square, you can multiply that number by four, then take off four." Algebraic formulas could be the focus of an extension activity for interested students who are ready to be extended.

17.

Slide twelve: At this point, students might be invited to create their own tukutuku pattern using the grid at the bottom of the copymaster. Alternatively, you might give them the challenging task on slide 12. Encourage the students to structure each pattern. For example, the rows of the tapatoru pattern contain 12 + 11 + 10 +…+ 3 + 2 + 1 crosses, which total 78 crosses. The pātiki pattern has a 5 x 5 array of black crosses and a 4 x 4 array of red crosses, so has a total of 25 + 16 = 41 crosses.

Matariki was a time when food was stored, and the weather was not always pleasant outside. So whānau (families) spent time together engaging in cultural pursuits such as storytelling, the arts, and games. A popular game for tamariki (children) was to make spinning tops. The tops were carved from hardwood, like mataī. A whip made from a stick and flax fibre was used to guide the top over obstacles and keep it spinning. A picture of a traditional top can be found at:

• Te Ara: Pōtaka tā (whip tops) 

There are cheap and accessible materials available to create tops. This video takes a scientific approach to making different tops: 

• How to: Build spinning tops with everyday objects

1.

Any plastic bottle top will work, e.g. milk bottle, yoghurt, marmite jar. Use bamboo skewers for the spindle (vertical part). You can trim the skewers to size, which is a nice variation when students are trying to ‘tune up’ their tops. Small nails or screws are cheap and safe for making the hole in the centre of the top. It is important not to make the hole too big. The skewer needs to be pushed firmly into the hole and checked to see if it is at right angles to the top (students will find that out in the tuning process). Adding weight to the spinner can also increase the spin time. Blu-Tac or plasticine is good for putting on the inside as it keeps the spindle vertical and the position of the weight can be altered. Take care. Not a lot of extra weight is needed, and it is very easy to unbalance the top.

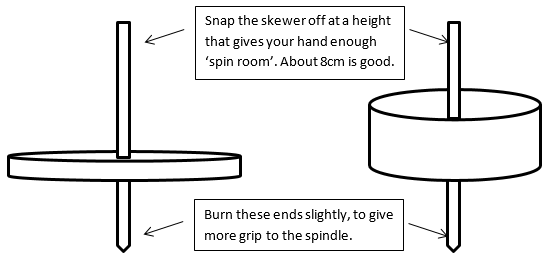
2.

The first mathematical challenge is finding the exact centre of a circle. Discuss what is likely to happen if the hole is not in the middle of the plastic bottle top. Since tops rely on balance, an off-centre top will not spin for long. Challenge the students to find a way to find the centre of a circle. You might give them some paper circles to experiment with. Rulers and pencils will also be helpful.

3.

Students are likely to suggest the ‘cross method’ of finding two diameters, one vertical and the other horizontal. This method is quite accurate, but it is not always easy to ensure the lines are actually diameters.

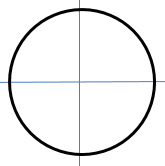
4.

Draw a large circle on the whiteboard and mark a point on the circumference. Put the zero mark of a metre-long ruler on the point and rotate the rule about it.

5.

Ask: 

• How will I know when the ruler is making a diameter?

Some students might notice changes to the measurement from the point to where the ruler crosses the other side. 

• If the measurement changes, how will I know when I have a diameter?

The ruler marks a diameter when the measure is at its greatest. The measure declines as the ruler is rotated from that position.

6.

You can now draw a diameter on the circle.

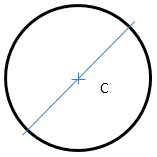
7.

Ask: 

• Where will the centre of the circle be?

The centre is at the midpoint of the diameter (C).

8.

Students can then make their spinning tops. Since this is a celebration of Māori culture, they might like to consider how the inside circle of the top might be decorated. 

9.

Ask: 

• What will happen to the design as you spin your top?

In fact, much specific detail will be lost as the top rotates, so encourage your students to keep the design simple. They could decorate directly onto the plastic with spirit-based pens by cutting a circle of paper the size of the top, decorating that and putting it inside the top is a safer option.

10.

This beautiful koru spiral top was made from a plastic yoghurt lid and spins for about one minute.

11.

Once you have a good collection of tops, emulate the competitive nature of traditional top spinning by having a contest. The goal is to have the top spin the longest. Allow your students to ‘tune up’ their tops. This activity will involve practising the turn of their fingers, trimming the length of the spindle, altering the length of the pointy section, and adding little amounts of weight. 

12.

The easiest way to time the tops is to put the students in pairs or threes. So as one student spins, the other students time the spinning. A top has finished spinning when it no longer turns at all because it is resting on its side. If you do not have sufficient stopwatches or devices with timers for the whole class, you could use group timing as a class. Count down to the start of the spin (e.g., "three, two, one, spin"). Count out the seconds from the start so the students know their top spin time from the last number before it stops. You could also teach students to use timers or stopwatches and have them record the times in this way.

13.

It is important to record the times of spins. This raises some issues:

• How accurate do we want to be? 
• Will each person get only one spin, or will they be allowed many spins?
• If many spins are allowed, which time is counted? (best, worst, middle, average, total)

14.

Once the class has made these decisions, give each student a square of paper to record their spin time. You could include other variables such as the origin of the lid (or diameter), length of the spindle point, length of the spindle handle, weights used? (Yes or No), etc. If you elect multiple variables, then creating a data card may be the best way to gather the data.

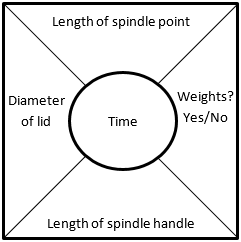
15.

Ask your students to put the squares of paper or data cards in the centre of a class circle. 

16.

Ask: 

• What could we do with this data?
• What questions could we ask?"

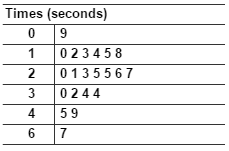
Students might come up with summary questions like "What is our average spin time?".
Since most of the variables are numeric, you might use dot plots or stem and leaf graphs to display the data. For example, to make a dot plot, use a skipping rope to make a long line and ask the students to order their cards along the line by time. Identical times can be arranged vertically on the same spot.

17.

Some students might suggest comparison questions such as:

• Do tops with weights spin longer than tops without weights?

Comparison questions can be investigated by creating a graph for each group (Yes and No) and comparing the distributions of times.

18.

Some students might suggest relationship questions such as:

• Is a shorter spindle point best for improving spin times?

You could put the data from both variables into a spreadsheet (e.g., using Microsoft Excel or Google Sheets) and graph the relationship using a scatter plot.

In this session, students investigate kōwhaiwhai patterns. One of the basic units of kōwhaiwhai is the koru, or fern frond. Nowadays, kōwhaiwhai refers to any figure generated using the koru but your students will investigate some of the designs found in wharenui (meeting houses). These designs are used on the tāhū (ridgepole) and heke (rafters). Tāhū and heke are the spine and ribs of the tipuna (ancestor) embodied in the wharenui, so kōwhaiwhai is a way to acknowledge the mana of that important person.

1.

Begin by drawing a simple koru. Spirals, like other stems in nature, usually obey the Fibonacci sequence, so that is a good way to start. Slide 1 of Matariki level 3-4 and Matariki L3-4 have a template for the Fibonacci spiral. Before clicking the animation, ask the students what they notice about the template.

2.

Some students might notice the circles.
Ask: 

• How big are the circles? The small circle is located inside the smallest square. Let’s call that one "square".

3.

Ask: 

• How big are the other squares?

Students might notice that the squares grow in a sequence, 1 x 1, 1 x 1, 2 x 2, 3 x 3, 5 x 5 (this is an interesting leap—why five?).

4.

Ask: 

• What square would the large circle fit into? (The 3 x 3 square)

5.

Students can then follow the animation to create a koru pattern. Show the students slide 2, which shows some examples of kōwhaiwhai. Note how the patterns have many koru and how the colours white, red, and black are used to convey meaning. Ask:

• How do you think the artist made these patterns?

Look for students to recognise that there is an element of repetition in each pattern. Discuss the transformations used. Students should easily be able to identify examples of translation and reflection.

6.

The next part can be completed better using a simple graphics computer package that allows the element to be copied and pasted repeatedly. Students can create a single element manually, and that element can be photocopied or scanned to form the whole pattern. 

7.

Give the students a rectangle of cardboard to create an element (File cards are good). This will form the repeating part of their pattern. Tell your students to create a koru design that starts in the left bottom corner and touches all four sides of the card. It is a good idea to rule up a grid on the card to help students keep the dimensions consistent.

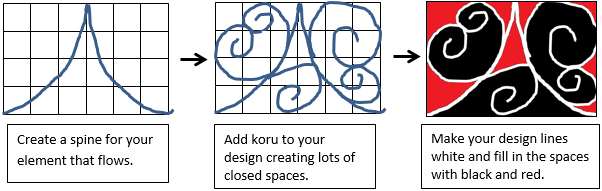
8.

Ask the students to name their elements, e.g. Te Maunga, and collect them for photocopying or scanning. Then look again at slide 3 of the PowerPoint. Discuss how the element has been moved to create each pattern. Expect students to use mathematical language like ‘translation’, and ‘reflection’ to describe the transformations. 

9.

Provide the students with copies or scans of their element. PowerPoint works well as a computer programme for copying the repeating pattern and performing transformations on it. Alternatively, students can cut and paste physical copies onto a strip of art paper. Six elements joined end-on-end by some transformation (translation, reflection, rotation) is a good size and allows other students to figure out which transformations have occurred.

10.

More information about the 7 types of frieze patterns is available in the teachers' notes for Kōwhaiwhai, an activity from page 14 of Figure It Out, Level 4, Geometry, Book One.

In this session, students investigate the geometry and measurement associated with the traditional game of Kī-o-Rahi. The game is based on the intrepid struggles of Rahi-tutaka-hina (Rahi for short) to rescue his wife, Ti Ara-kura-pake-wai, who was captured by the patupaiarehe (fair-skinned fairies). You can read the legend and an article about the game in School Journal, Part 2, Number 3, 2010. Click to download a literature unit based on the legend. 

The rules for Kī-o-Rahi vary a bit from place to place, but those variations are relatively minor. There is now a national championship for the game, where teams from all over Aotearoa gather to compete. An instructional video is available from the link below:

• How to play: Kī-o-Rahi (Rangatahi Tū Rangatira)

1.

The game is played with a soft ball called the kī. In older times, this was made of flax. Rahi was the hero in the legend. Like netball, Kī-o-Rahi is played in four quarters, with the teams taking it in turns to be Kīoma (guardians of the ki) and Taniwha. 

2.

Ask: 

• If we wanted the game to last for 60 minutes, how much time should we allow for each quarter? 

Quarters of 15 minutes each would allow little time for setting up, rest stops, and packing up, so quarters of ten minutes are the usual practice.

3.

Show the students Matariki L3-5. Ask them what they notice about the layout of the field for Kī-o-Rahi. Expect them to notice important features such as the concentric circles (same centre) that mark the zones, the centre target called te tupu, which represents the rock Rahi was sheltered on, and the seven pou (yellow cones) that represent the stars of Matariki. 

4.

Challenge the students to work out how they will mark out the field for Kī-o-Rahi. The journal article mentions that the class used a piece of skipping rope and a spray can to mark the circles. "How did they use the rope?" Remind the students that the pou are spread equally around the outer circle.

• How are you going to make sure that the pou are in the correct positions?

5.

Give the students a page of grid paper, some string (stand in for the rope), and a protractor to help them map out the field. Each square on the grid paper represents 1 square metre on the real field. Remind them that what they do on paper has to be ‘doable’ with large measures. Students can work in small groups of two or three to devise their plans.
Look for students to:

• Work out how to draw a circle by fixing one end of the string in the centre (Te Tupu) and walking around the circumference with the string kept taut;
• Use the scale on the grid paper to avoid measuring with a ruler;
• Consider how the pou might be located using either equal distance around the outer circle (string might be looped around the circle to measure the circumference) or using the protractor to divide 360° by seven.

6.

After an appropriate time of investigation, bring the class together to discuss their strategies. Focus on the properties of a circle (a set of points the same distance, the radius, from the centre), angles as measures of turn, and the use of scale. Pose problems with that scale.

• Imagine a Kioma player who runs in straight lines and touches all seven pou. How far does she run in metres to do that?

7.

Ask the students to mark a move that a player might make in the game. For example:

• A kioma player might touch two pou, then run around Te Ao into Te Ara and touch the ball on te tupu (2 goals!). How far does he run?
• A taniwha player throws the ball to a team member on the opposite side of Te Roto. That player throws the ball at te tupu and scores a tupu wairua (goal!). How far does the ball travel altogether in both throws?

8.

When the class has a well-developed plan for marking the field, grab the necessary equipment and play Kī-o-Rahi.