Getting in line
This is a level 2 geometry activity from the Figure It Out series. A PDF of the student activity is included.

About this resource
Figure It Out is a series of 80 books published between 1999 and 2009 to support teaching and learning in New Zealand classrooms.
This resource provides the teachers’ notes and answers for one activity from the Figure It Out series. A printable PDF of the student activity can be downloaded from the materials that come with this resource.
Specific learning outcomes:
- Identify the line of symmetry in two-dimensional shapes.
Getting in line
Achievement objectives
GM2-7: Predict and communicate the results of translations, reflections, and rotations on plane shapes.
Required materials
- Figure It Out, Level 2–3, Geometry, "Getting in line", page 15
- pattern blocks
- mirrors
See Materials that come with this resource to download:
- Getting in line activity (.pdf)
Activity
To begin the activity, students should trace around the pattern block they are considering so that they can draw in the lines of reflection (mirror lines). For a square, the four lines would be:

Some of the other pattern block shapes are more difficult to analyse (see diagrams in the Answers section).
Some students will draw lines that appear to cut the shape in half but are not lines of reflection symmetry. For example:
Students need to self-check these lines by looking at the whole shape and then comparing it with the image they see when they put a mirror on the mirror line.
Investigating the number of lines of symmetry of a circle is an interesting extension. Some students may colour the whole circle to show that there are so many lines that they couldn’t draw them all.
This is one way of describing infinity.
Finding lines of symmetry for shapes made from a number of pattern blocks is considerably more difficult than for single pattern block shapes. However, the same principles apply (see the diagrams in the Answers section).
The final challenge is to build pattern block shapes with specified numbers of lines of symmetry. In this case, students will need to consider the single-pattern block shapes once more. For example, building a pattern with three lines of symmetry will need to be based around a triangle or a hexagon shape. A pattern with four lines of symmetry will need to be based around a square shape. See the Answers section for examples.
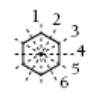
1.
2.
Triangle:
a.
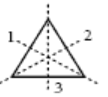
b. 3 mirror lines.
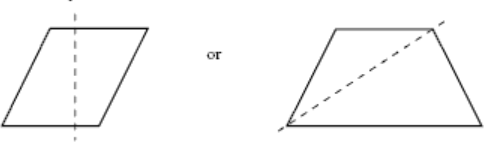
Rhombus:
a.

b. 2 mirror lines.
Trapezium:
a.

b. 1 mirror line.
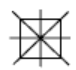
Hexagon:
a.
b. 6 mirror lines.
3.
a. 3 mirror lines.
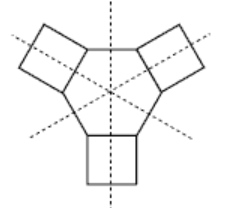
b. 1 mirror line.
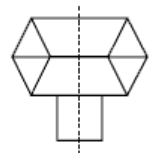
c. No mirror lines.
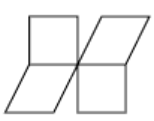
d. 4 mirror lines.
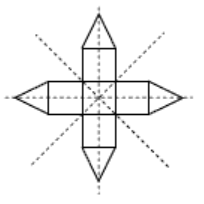
4.
Answers will vary. Some examples are:
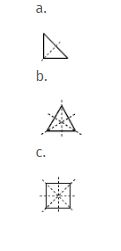
The quality of the images on this page may vary depending on the device you are using.


