Addition with hundreds and tens

1.

Pose initial problems in which only tens, then only hundreds, are added together. Use the context from the diagnostic question (i.e., people in the town) and alter the numbers. You might feel it is appropriate to include the name of a local or interesting town in the question.

• There are 60 people in the town of Millers Flat. 30 more people come to the town for the holidays. How many people are in the town now?

2.

Model the problem with Place Value People on a Place Value Board.

• How many tens make sixty?

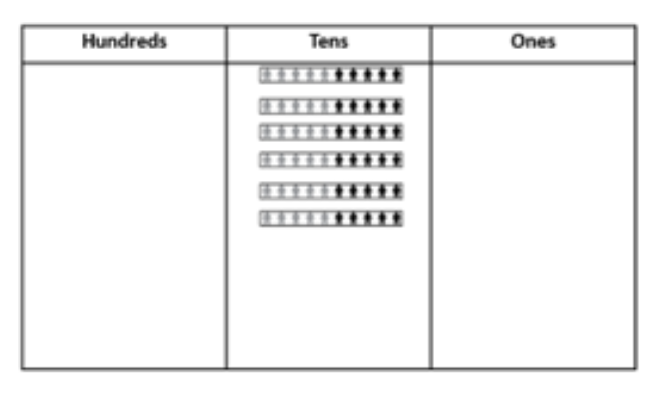
• Thirty more people come. How many tens is that? 
• How many people are in the town now?

3.

Model the operation with the Place Value People and record an algorithm and an equation.

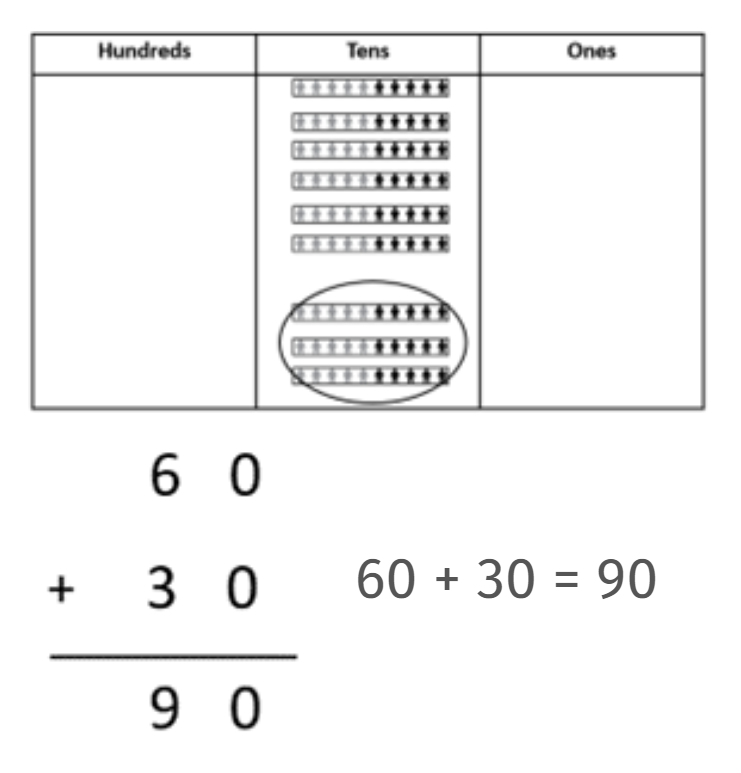
• What do you notice? 

Look for students to see that 6 + 3 = 9 can be used to find 60 + 30 = 90. You might emphasise this by modelling the addition of 6 and 3 place value people in the ones column of the place value board before drawing attention to the similarities between this model of 9 and the model of 90.

Use a calculator to model the sequence of pressing keys and to confirm the result.

4.

Provide other problems, altering the context as appropriate. Model each problem with materials (place value people and the three-column place value board), calculator sequences, equations, and a vertical written algorithm, as appropriate to the needs of your students. Avoid problems that require the naming of groups of tens and hundreds.

Groups of ten

• There are 30 people staying in the Millers Flat campground. 40 more people stay in motels. How many people are staying in Millers Flat?

Hundreds

• There are 400 people in the town of Ross. 300 more people come to the town for the holidays. How many people are in the town now?

• Look for students to see that their understanding of 4 + 3 = 7 can be applied to solve 400 + 300 = 700. Support this understanding by modelling the solving of both equations using materials.

Hundreds and tens

• There are 240 people staying in Springfield. 300 more people come to the town for the holidays. How many people are in the town now?

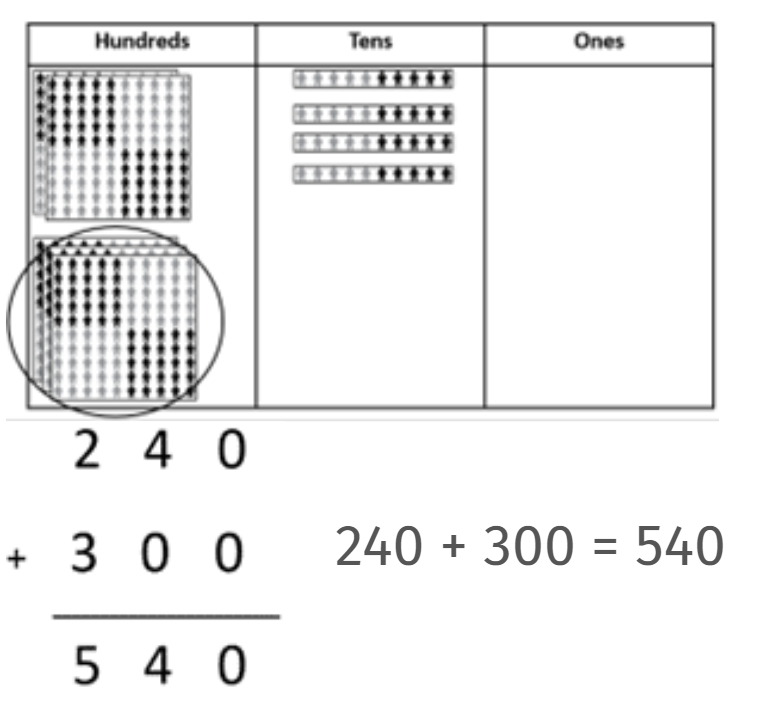
• Look for students to recognise that 2 + 3 = 5 can be applied to solve 200 + 300 = 500 and that 4 + 0 = 4 can be applied to solve 40 + 0 = 40. Support this understanding by modelling the solving of each pair of equations using materials. Students should also recognise the role of zero as a placeholder and a symbol for “nothing of something”.

5.

Vary the addends in the given problems to support students to act on units of one hundred and ten in the same way that they act on units of one. Examples might be:

• There are 90 people in the town. 600 more people come to the town for the holidays. How many people are in the town now?
• There are 370 people in the town. 120 more people come to the town for the holidays. How many people are in the town now?

1.

Practise the three key connections between words, numerals, and quantities until students are fluent in solving problems without materials. This should involve the efficient use of algorithms and equations to solve problems. You might model the use of materials for the students as they solve the problem or support some students to "fold back" to the use of materials to check their working. Reinforce understanding with the use of calculator sequences. For example:

• There are 530 people in the town. 240 more people come to the town for the holidays. How many people are in the town now?

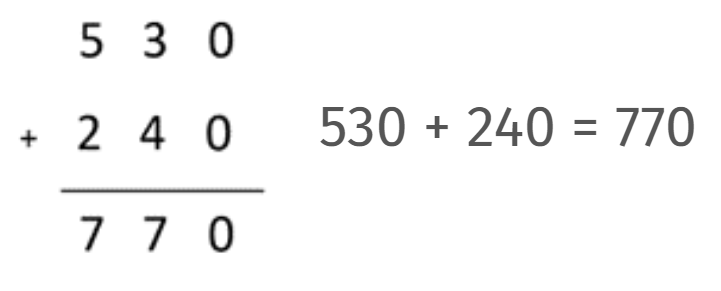
Pose problems that involve ones, with no renaming. For example:

• There are 420 people in the town. 68 more people come to the town for the holidays. How many people are in the town now?